I find this process easier to reason through by writing out a small 3-column version explicitly:
\begin{equation*}
\begin{bmatrix} A_{*0} & A_{*1} & A_{*2} \end{bmatrix} =
\begin{bmatrix} Q_{*0} & Q_{*1} & Q_{*2} \end{bmatrix} \begin{bmatrix}
R_{00} & R_{01} & R_{02} \\
& R_{11} & R_{12} \\
& & R_{22}
\end{bmatrix}
\end{equation*}
which gives:
\begin{align*}
&A_{*0} = Q_{*0} R_{00} \\
&A_{*1} = Q_{*0} R_{01} + Q_{*1} R_{11} \\
&A_{*2} = Q_{*0} R_{02} + Q_{*1} R_{12} + Q_{*2} R_{22}
\end{align*}
From this and the orthonormal properties of \(Q\), the meaning of the \(R_{ji}\) values are clear, the projection of the \(i\)'th column of \(A\) onto the \(j\)'th column of \(Q\). These allows fixing the values of \(R_{ji}\) and norms of \(Q_{*i}\):
- \(Q_{*i}^T Q_{*j} = 0, \forall i \neq j\): columns of \(Q\) are orthogonal so each \(R_{j*}\) value must account for entire parallel component of \(A_{*j}\) onto each column of \(Q\).
- \(\|Q_{*i}\|_2 = 1, \forall i\): constrains \(\|Q_{*i}\|\) and corresponding \(R_{ji}\) values.
Therefore:
- \(R_{00} = \|A_{*0}\|_2\) and \(Q_{*0} = A_{*0}/R_{00}\)
- \(R_{01} = Q_{*0}^T A_{*1}\), \(s_1 = A_{*1} - R_{01} Q_{*0}\), \(R_{11} = \|s_1\|_2\) \(Q_{*1} = s_1/R_{11}\)
- \(R_{02} = Q_{*0}^T A_{*2},~R_{12} = Q_{*1}^T A_{*2}, s_2 = A_{*2} - R_{02} Q_{*0} - R_{12} Q_{*1}, R_{22} = \| s_2 \|_2, Q_{*2} = s_2/R_{22}\)
or in general:
- \(R_{ji} = Q_{*j}^T A_{*i}, \forall j < i\)
- \(s_{i} = A_{*i} - \sum_j R_{ji} Q_{*j}\)
- \(R_{ii} = \| s_{i} \|_2, Q_{*i} = s_i/R_{ii}\)
and in python:
def qr_gs( A, inplace=True ):
'''Decompose A into Q*R with Q orthonormal and R upper triangular using classical Gram-Schmidt (unstable)'''
A = A if inplace else A.copy()
R = np.zeros((A.shape[1],A.shape[1]))
for i in range( A.shape[1] ):
for j in range(i):
R[j,i] = np.sum(A[:,j]*A[:,i])
A[:,i] -= R[j,i]*A[:,j]
R[i,i] = np.linalg.norm(A[:,i])
A[:,i] /= R[i,i]
return A,R
The form above generates \(Q\) column by column but has stability issues due to the use of classical Gram-Schmidt. It can be improved by replacing classical Gram-Schmidt with modified Gram-Schmidt:
def qr_mgs( A, inplace=True ):
'''Decompose A into Q*R with Q orthonormal and R upper triangular using modified Gram-Schmidt
Assumes columns of A are linearly independent.
'''
A = A if inplace else A.copy()
R = np.zeros((A.shape[1],A.shape[1]))
for i in range( A.shape[1] ):
R[i,i] = np.linalg.norm(A[:,i])
A[:,i] /= R[i,i]
for j in range(i+1,A.shape[1]):
R[i,j] = np.dot(A[:,j],A[:,i])
A[:,j] -= R[i,j]*A[:,i]
return A,R
The inner loop of this can be replaced entirely with vectorization in python but the above form gives a reasonable starting point for porting to another language like C or C++. These implementations should also check for \(R_{ii} = 0\) which indicate a rank deficient system.
It's pretty useful to be able to load meshes when doing graphics. One format that is nearly ubiquitous are Wavefront .OBJ files, due largely to their good features-to-complexity ratio. Sure there are better formats, but when you just want to get a mesh into a program it's hard to beat .obj which can be imported and exported from just about anyhwere.
The code below loads and saves .obj files, including material assignments (but not material parameters), normals, texture coordinates and faces of any number of vertices. It supports faces with/without either/both of normals and texture coordinates and (if you can accept 6D vertices) also suports per-vertex colors (a non-standard extension sometimes used for debugging in mesh processing). Faces without either normals or tex-coords assign the invalid value -1 for these entries.
From the returned object, it is pretty easy to do things like sort faces by material indices, split vertices based on differing normals or along texture boundaries and so on. It also has the option to tesselate non-triangular faces, although this only works for convex faces (you should only be using convex faces anyway though!).
# wavefront.py
import numpy as np
class WavefrontOBJ:
def __init__( self, default_mtl='default_mtl' ):
self.path = None # path of loaded object
self.mtllibs = [] # .mtl files references via mtllib
self.mtls = [ default_mtl ] # materials referenced
self.mtlid = [] # indices into self.mtls for each polygon
self.vertices = [] # vertices as an Nx3 or Nx6 array (per vtx colors)
self.normals = [] # normals
self.texcoords = [] # texture coordinates
self.polygons = [] # M*Nv*3 array, Nv=# of vertices, stored as vid,tid,nid (-1 for N/A)
def load_obj( filename: str, default_mtl='default_mtl', triangulate=False ) -> WavefrontOBJ:
"""Reads a .obj file from disk and returns a WavefrontOBJ instance
Handles only very rudimentary reading and contains no error handling!
Does not handle:
- relative indexing
- subobjects or groups
- lines, splines, beziers, etc.
"""
# parses a vertex record as either vid, vid/tid, vid//nid or vid/tid/nid
# and returns a 3-tuple where unparsed values are replaced with -1
def parse_vertex( vstr ):
vals = vstr.split('/')
vid = int(vals[0])-1
tid = int(vals[1])-1 if len(vals) > 1 and vals[1] else -1
nid = int(vals[2])-1 if len(vals) > 2 else -1
return (vid,tid,nid)
with open( filename, 'r' ) as objf:
obj = WavefrontOBJ(default_mtl=default_mtl)
obj.path = filename
cur_mat = obj.mtls.index(default_mtl)
for line in objf:
toks = line.split()
if not toks:
continue
if toks[0] == 'v':
obj.vertices.append( [ float(v) for v in toks[1:]] )
elif toks[0] == 'vn':
obj.normals.append( [ float(v) for v in toks[1:]] )
elif toks[0] == 'vt':
obj.texcoords.append( [ float(v) for v in toks[1:]] )
elif toks[0] == 'f':
poly = [ parse_vertex(vstr) for vstr in toks[1:] ]
if triangulate:
for i in range(2,len(poly)):
obj.mtlid.append( cur_mat )
obj.polygons.append( (poly[0], poly[i-1], poly[i] ) )
else:
obj.mtlid.append(cur_mat)
obj.polygons.append( poly )
elif toks[0] == 'mtllib':
obj.mtllibs.append( toks[1] )
elif toks[0] == 'usemtl':
if toks[1] not in obj.mtls:
obj.mtls.append(toks[1])
cur_mat = obj.mtls.index( toks[1] )
return obj
def save_obj( obj: WavefrontOBJ, filename: str ):
"""Saves a WavefrontOBJ object to a file
Warning: Contains no error checking!
"""
with open( filename, 'w' ) as ofile:
for mlib in obj.mtllibs:
ofile.write('mtllib {}\n'.format(mlib))
for vtx in obj.vertices:
ofile.write('v '+' '.join(['{}'.format(v) for v in vtx])+'\n')
for tex in obj.texcoords:
ofile.write('vt '+' '.join(['{}'.format(vt) for vt in tex])+'\n')
for nrm in obj.normals:
ofile.write('vn '+' '.join(['{}'.format(vn) for vn in nrm])+'\n')
if not obj.mtlid:
obj.mtlid = [-1] * len(obj.polygons)
poly_idx = np.argsort( np.array( obj.mtlid ) )
cur_mat = -1
for pid in poly_idx:
if obj.mtlid[pid] != cur_mat:
cur_mat = obj.mtlid[pid]
ofile.write('usemtl {}\n'.format(obj.mtls[cur_mat]))
pstr = 'f '
for v in obj.polygons[pid]:
# UGLY!
vstr = '{}/{}/{} '.format(v[0]+1,v[1]+1 if v[1] >= 0 else 'X', v[2]+1 if v[2] >= 0 else 'X' )
vstr = vstr.replace('/X/','//').replace('/X ', ' ')
pstr += vstr
ofile.write( pstr+'\n')
A function that round-trips the loader is shown below, the resulting mesh dump.obj can be loaded into Blender and show the same material ids and texture coordinates. If you inspect it (and remove comments) you will see that the arrays match the string in the function:
from wavefront import *
def obj_load_save_example():
data = '''
# slightly edited blender cube
mtllib cube.mtl
v 1.000000 1.000000 -1.000000
v 1.000000 -1.000000 -1.000000
v 1.000000 1.000000 1.000000
v 1.000000 -1.000000 1.000000
v -1.000000 1.000000 -1.000000
v -1.000000 -1.000000 -1.000000
v -1.000000 1.000000 1.000000
v -1.000000 -1.000000 1.000000
vt 0.625000 0.500000
vt 0.875000 0.500000
vt 0.875000 0.750000
vt 0.625000 0.750000
vt 0.375000 0.000000
vt 0.625000 0.000000
vt 0.625000 0.250000
vt 0.375000 0.250000
vt 0.375000 0.250000
vt 0.625000 0.250000
vt 0.625000 0.500000
vt 0.375000 0.500000
vt 0.625000 0.750000
vt 0.375000 0.750000
vt 0.125000 0.500000
vt 0.375000 0.500000
vt 0.375000 0.750000
vt 0.125000 0.750000
vt 0.625000 1.000000
vt 0.375000 1.000000
vn 0.0000 0.0000 -1.0000
vn 0.0000 1.0000 0.0000
vn 0.0000 0.0000 1.0000
vn -1.0000 0.0000 0.0000
vn 1.0000 0.0000 0.0000
vn 0.0000 -1.0000 0.0000
usemtl mat1
# no texture coordinates
f 6//1 5//1 1//1 2//1
usemtl mat2
f 1/5/2 5/6/2 7/7/2 3/8/2
usemtl mat3
f 4/9/3 3/10/3 7/11/3 8/12/3
usemtl mat4
f 8/12/4 7/11/4 5/13/4 6/14/4
usemtl mat5
f 2/15/5 1/16/5 3/17/5 4/18/5
usemtl mat6
# no normals
f 6/14 2/4 4/19 8/20
'''
with open('test_cube.obj','w') as obj:
obj.write( data )
obj = load_obj( 'test_cube.obj' )
save_obj( obj, 'dump.obj' )
if __name__ == '__main__':
obj_load_save_example()
Hope it's useful!
These are collections of functions that I end up re-implementing frequently.
import numpy as np
def manifold_mesh_neighbors( tris: np.ndarray ) -> np.ndarray:
"""Returns an array of triangles neighboring each triangle
Args:
tris (Nx3 int array): triangle vertex indices
Returns:
nbrs (Nx3 int array): neighbor triangle indices,
or -1 if boundary edge
"""
if tris.shape[1] != 3:
raise ValueError('Expected a Nx3 array of triangle vertex indices')
e2t = {}
for idx,(a,b,c) in enumerate(tris):
e2t[(b,a)] = idx
e2t[(c,b)] = idx
e2t[(a,c)] = idx
nbr = np.full(tris.shape,-1,int)
for idx,(a,b,c) in enumerate(tris):
nbr[idx,0] = e2t[(a,b)] if (a,b) in e2t else -1
nbr[idx,1] = e2t[(b,c)] if (b,c) in e2t else -1
nbr[idx,2] = e2t[(c,a)] if (c,a) in e2t else -1
return nbr
if __name__ == '__main__':
tris = np.array((
(0,1,2),
(0,2,3)
),int)
nbrs = manifold_mesh_neighbors( tris )
tar = np.array((
(-1,-1,1),
(0,-1,-1)
),int)
if not np.allclose(nbrs,tar):
raise ValueError('uh oh.')
These are collections of functions that I end up re-implementing frequently.
from typing import *
import numpy as np
def closest_rotation( M: np.ndarray ):
U,s,Vt = np.linalg.svd( M[:3,:3] )
if np.linalg.det(U@Vt) < 0:
Vt[2] *= -1.0
return U@Vt
def mat2quat( M: np.ndarray ):
if np.abs(np.linalg.det(M[:3,:3])-1.0) > 1e-5:
raise ValueError('Matrix determinant is not 1')
if np.abs( np.linalg.norm( M[:3,:3].T@M[:3,:3] - np.eye(3)) ) > 1e-5:
raise ValueError('Matrix is not orthogonal')
w = np.sqrt( 1.0 + M[0,0]+M[1,1]+M[2,2])/2.0
x = (M[2,1]-M[1,2])/(4*w)
y = (M[0,2]-M[2,0])/(4*w)
z = (M[1,0]-M[0,1])/(4*w)
return np.array((x,y,z,w),float)
def quat2mat( q: np.ndarray ):
qx,qy,qz,qw = q/np.linalg.norm(q)
return np.array((
(1 - 2*qy*qy - 2*qz*qz, 2*qx*qy - 2*qz*qw, 2*qx*qz + 2*qy*qw),
( 2*qx*qy + 2*qz*qw, 1 - 2*qx*qx - 2*qz*qz, 2*qy*qz - 2*qx*qw),
( 2*qx*qz - 2*qy*qw, 2*qy*qz + 2*qx*qw, 1 - 2*qx*qx - 2*qy*qy),
))
if __name__ == '__main__':
for i in range( 1000 ):
q = np.random.standard_normal(4)
q /= np.linalg.norm(q)
A = quat2mat( q )
s = mat2quat( A )
if np.linalg.norm( s-q ) > 1e-6 and np.linalg.norm( s+q ) > 1e-6:
raise ValueError('uh oh.')
R = closest_rotation( A+np.random.standard_normal((3,3))*1e-6 )
if np.linalg.norm(A-R) > 1e-5:
print( np.linalg.norm( A-R ) )
raise ValueError('uh oh.')
Python is a pretty nice language for prototyping and (with numpy and scipy) can be quite fast for numerics but is not great for algorithms with frequent tight loops. One place I run into this frequently is in graphics, particularly applications involving meshes.
Not much can be done if you need to frequently modify mesh structure. Luckily, many algorithms operate on meshes with fixed structure. In this case, expressing algorithms in terms of block operations can be much faster. Actually implementing methods in this way can be tricky though.
To gain more experience in this, I decided to try implementing the As-Rigid-As-Possible Surface Modeling mesh deformation algorithm in Python. This involves solving moderately sized Laplace systems where the right-hand-side involves some non-trivial computation (per-vertex SVDs embedded within evaluation of the Laplace operator). For details on the algorithm, see the link.
As it turns out, the entire implementation ended up being just 99 lines and solves 1600 vertex problems in just under 20ms (more on this later). Full code is available.
Building the Laplace operator
ARAP uses cotangent weights for the Laplace operator in order to be relatively independent of mesh grading. These weights are functions of the angles opposite the edges emanating from each vertex. Building this operator using loops is slow but can be sped up considerably by realizing that every triangle has exactly 3 vertices, 3 angles and 3 edges. Operations can be evaluated on triangles and accumulated to edges.
Here's the Python code for a cotangent Laplace operator:
from typing import *
import numpy as np
import scipy.sparse as sparse
import scipy.sparse.linalg as spla
def build_cotan_laplacian( points: np.ndarray, tris: np.ndarray ):
a,b,c = (tris[:,0],tris[:,1],tris[:,2])
A = np.take( points, a, axis=1 )
B = np.take( points, b, axis=1 )
C = np.take( points, c, axis=1 )
eab,ebc,eca = (B-A, C-B, A-C)
eab = eab/np.linalg.norm(eab,axis=0)[None,:]
ebc = ebc/np.linalg.norm(ebc,axis=0)[None,:]
eca = eca/np.linalg.norm(eca,axis=0)[None,:]
alpha = np.arccos( -np.sum(eca*eab,axis=0) )
beta = np.arccos( -np.sum(eab*ebc,axis=0) )
gamma = np.arccos( -np.sum(ebc*eca,axis=0) )
wab,wbc,wca = ( 1.0/np.tan(gamma), 1.0/np.tan(alpha), 1.0/np.tan(beta) )
rows = np.concatenate(( a, b, a, b, b, c, b, c, c, a, c, a ), axis=0 )
cols = np.concatenate(( a, b, b, a, b, c, c, b, c, a, a, c ), axis=0 )
vals = np.concatenate(( wab, wab,-wab,-wab, wbc, wbc,-wbc,-wbc, wca, wca,-wca, -wca), axis=0 )
L = sparse.coo_matrix((vals,(rows,cols)),shape=(points.shape[1],points.shape[1]), dtype=float).tocsc()
return L
Inputs are float \(3 \times N_{verts}\) and integer \(N_{tris} \times 3\) arrays for vertices and triangles respectively. The code works by making arrays containing vertex indices and positions for all triangles, then computes and normalizes edges and finally computes angles and cotangents. Once the cotangents are available, initialization arrays for a scipy.sparse.coo_matrix are constructed and the matrix built. The coo_matrix is intended for finite-element matrices so it accumulates rather than overwrites duplicate values. The code is definitely faster and most likely fewer lines than a loop based implementation.
Evaluating the Right-Hand-side
The Laplace operator is just a warm-up exercise compared to the right-hand-side computation. This involves:
- For every vertex, collecting the edge-vectors in its one-ring in both original and deformed coordinates
- Computing the rotation matrices that optimally aligns these neighborhoods, weighted by the Laplacian edge weights, per-vertex. This involves a SVD per-vertex.
- Rotating the undeformed neighborhoods by the per-vertex rotation and summing the contributions.
In order to vectorize this, I constructed neighbor and weight arrays for the Laplace operator. These store the neighboring vertex indices and the corresponding (positive) weights from the Laplace operator. A catch is that vertices have different numbers of neighbors. To address this I use fixed sized arrays based on the maximum valence in the mesh. These are initialized with default values of the vertex ids and weights of zero so that unused vertices contribute nothing and do not affect matrix structure.
To compute the rotation matrices, I used some index magic to accumulate the weighted neighborhoods and rely on numpy's batch SVD operation to vectorize over all vertices. Finally, I used the same index magic to rotate the neighborhoods and accumulate the right-hand-side.
The code to accumulate the neighbor and weight arrays is:
def build_weights_and_adjacency( points: np.ndarray, tris: np.ndarray, L: Optional[sparse.csc_matrix]=None ):
L = L if L is not None else build_cotan_laplacian( points, tris )
n_pnts, n_nbrs = (points.shape[1], L.getnnz(axis=0).max()-1)
nbrs = np.ones((n_pnts,n_nbrs),dtype=int)*np.arange(n_pnts,dtype=int)[:,None]
wgts = np.zeros((n_pnts,n_nbrs),dtype=float)
for idx,col in enumerate(L):
msk = col.indices != idx
indices = col.indices[msk]
values = col.data[msk]
nbrs[idx,:len(indices)] = indices
wgts[idx,:len(indices)] = -values
Rather than break down all the other steps individually, here is the code for an ARAP class:
class ARAP:
def __init__( self, points: np.ndarray, tris: np.ndarray, anchors: List[int], anchor_weight: Optional[float]=10.0, L: Optional[sparse.csc_matrix]=None ):
self._pnts = points.copy()
self._tris = tris.copy()
self._nbrs, self._wgts, self._L = build_weights_and_adjacency( self._pnts, self._tris, L )
self._anchors = list(anchors)
self._anc_wgt = anchor_weight
E = sparse.dok_matrix((self.n_pnts,self.n_pnts),dtype=float)
for i in anchors:
E[i,i] = 1.0
E = E.tocsc()
self._solver = spla.factorized( ( self._L.T@self._L + self._anc_wgt*E.T@E).tocsc() )
@property
def n_pnts( self ):
return self._pnts.shape[1]
@property
def n_dims( self ):
return self._pnts.shape[0]
def __call__( self, anchors: Dict[int,Tuple[float,float,float]], num_iters: Optional[int]=4 ):
con_rhs = self._build_constraint_rhs(anchors)
R = np.array([np.eye(self.n_dims) for _ in range(self.n_pnts)])
def_points = self._solver( self._L.T@self._build_rhs(R) + self._anc_wgt*con_rhs )
for i in range(num_iters):
R = self._estimate_rotations( def_points.T )
def_points = self._solver( self._L.T@self._build_rhs(R) + self._anc_wgt*con_rhs )
return def_points.T
def _estimate_rotations( self, def_pnts: np.ndarray ):
tru_hood = (np.take( self._pnts, self._nbrs, axis=1 ).transpose((1,0,2)) - self._pnts.T[...,None])*self._wgts[:,None,:]
rot_hood = (np.take( def_pnts, self._nbrs, axis=1 ).transpose((1,0,2)) - def_pnts.T[...,None])
U,s,Vt = np.linalg.svd( rot_hood@tru_hood.transpose((0,2,1)) )
R = U@Vt
dets = np.linalg.det(R)
Vt[:,self.n_dims-1,:] *= dets[:,None]
R = U@Vt
return R
def _build_rhs( self, rotations: np.ndarray ):
R = (np.take( rotations, self._nbrs, axis=0 )+rotations[:,None])*0.5
tru_hood = (self._pnts.T[...,None]-np.take( self._pnts, self._nbrs, axis=1 ).transpose((1,0,2)))*self._wgts[:,None,:]
rhs = np.sum( (R@tru_hood.transpose((0,2,1))[...,None]).squeeze(), axis=1 )
return rhs
def _build_constraint_rhs( self, anchors: Dict[int,Tuple[float,float,float]] ):
f = np.zeros((self.n_pnts,self.n_dims),dtype=float)
f[self._anchors,:] = np.take( self._pnts, self._anchors, axis=1 ).T
for i,v in anchors.items():
if i not in self._anchors:
raise ValueError('Supplied anchor was not included in list provided at construction!')
f[i,:] = v
return f
The indexing was tricky to figure out. Error handling and input checking can obviously be improved. Something I'm not going into are the handling of anchor vertices and the overall quadratic forms that are being solved.
So does it Work?
Yes. Here is a 2D equivalent to the bar example from the paper:
import time
import numpy as np
import matplotlib.pyplot as plt
import arap
def grid_mesh_2d( nx, ny, h ):
x,y = np.meshgrid( np.linspace(0.0,(nx-1)*h,nx), np.linspace(0.0,(ny-1)*h,ny))
idx = np.arange(nx*ny,dtype=int).reshape((ny,nx))
quads = np.column_stack(( idx[:-1,:-1].flat, idx[1:,:-1].flat, idx[1:,1:].flat, idx[:-1,1:].flat ))
tris = np.vstack((quads[:,(0,1,2)],quads[:,(0,2,3)]))
return np.row_stack((x.flat,y.flat)), tris, idx
nx,ny,h = (21,5,0.1)
pnts, tris, ix = grid_mesh_2d( nx,ny,h )
anchors = {}
for i in range(ny):
anchors[ix[i,0]] = ( 0.0, i*h)
anchors[ix[i,1]] = ( h, i*h)
anchors[ix[i,nx-2]] = (h*nx*0.5-h, h*nx*0.5+i*h)
anchors[ix[i,nx-1]] = ( h*nx*0.5, h*nx*0.5+i*h)
deformer = arap.ARAP( pnts, tris, anchors.keys(), anchor_weight=1000 )
start = time.time()
def_pnts = deformer( anchors, num_iters=2 )
end = time.time()
plt.triplot( pnts[0], pnts[1], tris, 'k-', label='original' )
plt.triplot( def_pnts[0], def_pnts[1], tris, 'r-', label='deformed' )
plt.legend()
plt.title('deformed in {:0.2f}ms'.format((end-start)*1000.0))
plt.show()
The result of this script is the following:
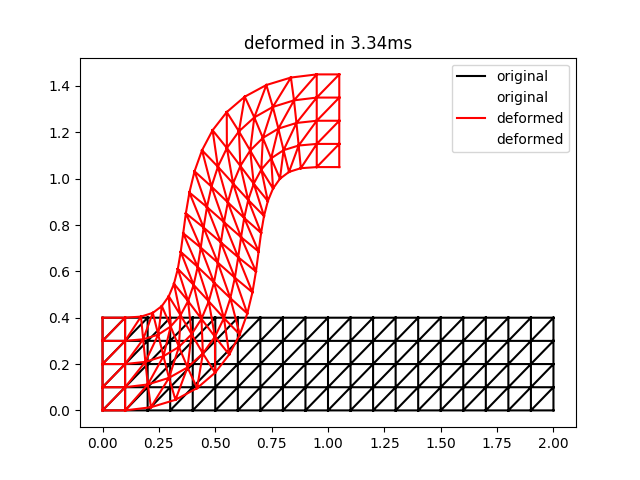
This is qualitatively quite close to the result for two iterations in Figure 3 of the ARAP paper. Note that the timings may be a bit unreliable for such a small problem size.
A corresponding result for 3D deformations is here (note that this corrects an earlier bug in rotation computations for 3D):

This process follows this link . First update apt and install docker.io
$ sudo apt-get update
$ sudo apt install docker.io
Next start the service and enable it at boot time:
$ sudo systemctl start docker
$ sudo systemctl enable docker
Finally add your current user to the docker group:
$ sudo usermod -a -G docker $USER
and log out of your account and back in.
Create Dockerfile
Create a blank Dockerfile
and then edit it to look like the following:
# start with ubuntu
FROM ubuntu:16.04
# update the software repository
RUN apt-get update
RUN apt-get install -y python3-dev
# add user appuser and switch to it
RUN useradd -ms /bin/bash appuser
USER appuser
WORKDIR /home/appuser
# copy over a test message and python
# script to print it to the screen
COPY data/ ./data/
COPY print_message.py .
# run the script at container startup
CMD ["python3", "print_message.py"]
Next make a directory to share with the image and put a simple message file into it.
$ mkdir data
$ echo "Hello from docker" > data/message.txt
Then create a python script to print the message:
if __name__ == '__main__':
with open('data/message.txt') as f:
data = f.read()
print( data )
Build the image and run it:
$ docker build -t test_image
$ docker run -it test_image
Hello from docker
And that's all there is to it.
In the previous part of this post I introduced deconvolution and built up the core of a total-variation deconvolution algorithm based on ADMM.
def deconvolve_ADMM( K, B, num_iters=40, rho=1.0, gamma=0.1 ):
# store the image size
dim = B.shape
# pad out the kernel if its the wrong shape
if K.shape != dim:
raise ValueError('B and K must have same shape')
# define the two derivative operators
Dx = Kernel2D( [ 0, 0], [-1, 0], [-1.0, 1.0] )
Dy = Kernel2D( [-1, 0], [ 0, 0], [-1.0, 1.0] )
# define an initial solution estimate
I = numpy.zeros( dim )
# define the two splitting variables and lagrangr multipliers
Zx = Dx.mul( I )
Zy = Dy.mul( I )
Ux = numpy.zeros( Zx.shape )
Uy = numpy.zeros( Zy.shape )
# cache the necessary terms for the I update, need to circularly
# shift the kernel so it's DC spot lies at the corner
fK = numpy.fft.fft2( numpy.roll( K/numpy.sum(K), (dim[0]//2,dim[1]//2), axis=(0,1) ) )
fB = numpy.fft.fft2( B )
fDx = Dx.spectrum( dim )
fDy = Dy.spectrum( dim )
# build the numerator and denominator
num_init = numpy.conj( fK )*fB
den = numpy.conj( fK )*fK + rho*( numpy.conj(fDx)*fDx + numpy.conj(fDy)*fDy )
# define the L1 soft-thresholding operator
soft_threshold = lambda q: numpy.sign(q)*numpy.maximum( numpy.abs( q ) - gamma/rho, 0.0 )
# main solver loop
for iter in range( num_iters ):
print('ADMM iteration [%d/%d]'%(iter,num_iters))
# I-update
V = rho*( Dx.mul( Zx - Ux, trans=True) + Dy.mul( Zy - Uy, trans=True ) )
I = numpy.real( numpy.fft.ifft2( (num_init + numpy.fft.fft2(V))/den ) )
# Z-updates, cache the gradient filter results
tmp_x = Dx.mul( I )
tmp_y = Dy.mul( I )
Zx = soft_threshold( tmp_x + Ux )
Zy = soft_threshold( tmp_y + Uy )
# multiplier update
Ux += tmp_x - Zx
Uy += tmp_y - Zy
# return reconstructed result
return I
That is it.
Deconvolution is the process of removing blur from a signal. For images, there are two main types:
- Blind deconvolution removes blur without specific knowledge of what the exact blur is. It generally requires estimating the blur kernel.
- Non-blind deconvolution removes blur but is provided the blur kernel directly. It is an easier problem than blind deconvolution. Non-blind deconvolution is often used as a component of blind deconvolution algorithms.
Here I am focusing on non-blind deconvolution.
Optimizing for \({\bf I}\)
Making the typical assumption of \(\epsilon\) being Gaussian noise, a solution for the sharp image \({\bf I}\) can be found by looking for an underlying sharp image that best explains, in a least-squares sense, the measured data \({\bf B}\).
\begin{equation*}
{\bf I} = \mbox{argmin}_{\bf I} \frac{1}{2} \| {\bf K} \otimes {\bf I} - {\bf B} \|_2^2
\end{equation*}
Denoting \(\mathcal{F}(\bf K)\) and \(\mathcal{F}^{-1}(\bf K)\) as the forward and inverse Fourier transform of \({\bf K}\) and \(*\) as complex conjugation, this equation can be solved very quickly in the Fourier domain:
\begin{equation*}
{\bf I} = \mathcal{F}^{-1}\left[ \frac{\mathcal{F}({\bf K})^*\mathcal{F}(\bf B)}{\mathcal{F}({\bf K})^2} \right]
\end{equation*}
Unfortunately the results are garbage. Zero or very low magnitude values of the Fourier transform of \({\bf K}\) cause divide-by-zero issues and amplify noise. These tiny values are due to convolution by \({\bf K}\) attenuating certain frequency bands to nothing. It makes sense intuitively since blurry images lose the sharp edges and fine details of focused images so the Fourier modes representing these are lost forever. Trying to undo the process is poorly defined and so the solve above just finds anything that minimizes the objective, whether it looks like an image or not.
It's possible to stabilize the above a bit by adding fudge factors here and there but the results are not very compelling. A better approach is to add regularizers to the optimization that favor specific types of underlying sharp images. One very effective set is the total variation which is incorporated below:
\begin{equation*}
{\bf I} = \mbox{argmin}_{\bf I} \frac{1}{2} \| {\bf K} \otimes {\bf I} - {\bf B} \|_2^2 + \gamma \| \frac{\partial}{\partial x} {\bf I} \|_1 + \gamma \| \frac{\partial}{\partial y} {\bf I} \|_1
\end{equation*}
The two extra terms penalize the gradients of the image and reach a zero value only for images that are constant. Using a 1-norm makes them less sensitive to large jumps in value than a 2-norm would be which makes these priors favor piecewise constant reconstructions. This is qualitatively similar to natural images that feature piecewise smooth features.
The only problem is that these 1-norm terms make the optimization much more difficult and costly to solve. However, the effort is worth it.
Formulating the Optimization with ADMM
The problem with solving the optimization above is that the 1-norm terms are non-smooth. This is challenging for optimization methods. Fortunately, there are some very effective tools for solving 1-norm problems in isolation and a framework call the Alternating Direction Method of Multipliers can be used to transform intractible monolithic objective functions (such as the one above) into several coupled simpler problems.
By being careful about which terms go where, this can result in very efficient solves for problems involving complex priors. What follows is only one option for the above problem.
The overall goal is to split the \(L_1\) solves into separate pixel-wise solves. This is done by introducing new variables and constraints that make the problem look more complex but actually help. The data term will stay as a coupled \(L_2\) problem and will absorb the coupling terms as well (which are also \(L_2\)) and serve to stabilize the solve.
The first step is to isolate the \(L_1\) terms. The differential operators in the priors have the effect of coupling all pixels to each other, but the fast solvers for \(L_1\) problems expect terms that look like \(\|{\bf A}\|_1\) for some image \({\bf A}\). This can be accomplished by introducing splitting variables \({\bf Z}_x,{\bf Z}_y\) with appropriate constraints.
\begin{align*}
{\bf I} = \mbox{argmin} & & \frac{1}{2} \| {\bf K} \otimes {\bf I} - {\bf B} \|_2^2 + \gamma \| {\bf Z}_x \|_1 + \gamma \| {\bf Z}_y \|_1 \\
\mbox{subject to} & & \frac{\partial}{\partial x} {\bf I} - {\bf Z}_x = 0 \\
& & \frac{\partial}{\partial y} {\bf I} - {\bf Z}_y = 0
\end{align*}
It is also important to make sure that the \({\bf Z}_x, {\bf Z}_y\) terms appear without complex linear operators in the constraints. This ensures that the terms will diagonalize to a large set of pixelwise 1D optimizations rather than couple together.
With the splitting variables introduced, the constraints can be incorporated into the objective via penalty terms with (scaled) Lagrange multipliers \({\bf U}_x,{\bf U}_y\). The multipliers keep the constraints stiff. Without the multipliers, the high weights needed on the penalty terms to enforce the constraints can dominate the solves.
Applying this step transform back from a constrained problem to a (much more complicated) unconstrained problem again:
\begin{equation*}
{\bf I} = \mbox{argmin} \frac{1}{2} \| {\bf K} \otimes {\bf I} - {\bf B} \|_2^2 + \frac{\rho}{2} \| \frac{\partial}{\partial x} {\bf I} - {\bf Z}_x + {\bf U}_x \|_2^2 + \frac{\rho}{2} \| \frac{\partial}{\partial y} {\bf I} - {\bf Z}_y + {\bf U}_y \|_2^2 + \gamma \| {\bf Z}_x \|_1 + \gamma \| {\bf Z}_y \|_1
\end{equation*}
This looks like a mess, but is just the original data term, the two added \(L_1\) terms and two additional \(L_2\) coupling terms. Calling the whole thing \(F({\bf I},{\bf Z}_x, {\bf Z}_y, {\bf U}_x, {\bf U}_y)\) the ADMM algorithm solves this by the following steps:
- Updates \({\bf I}\) by solving \({\bf I} = \mbox{argmin}_{\bf I} F({\bf I},{\bf Z}_x, {\bf Z}_y, {\bf U}_x, {\bf U}_y)\)
- Updates \({\bf Z}_x\) by solving \({\bf Z}_x = \mbox{argmin}_{{\bf Z}_x} F({\bf I},{\bf Z}_x, {\bf Z}_y, {\bf U}_x, {\bf U}_y)\)
- Updates \({\bf U}_x\) by setting \({\bf U}_x = {\bf U}_x + \frac{\partial}{\partial x} {\bf I} - {\bf Z}_x\)
- Repeats the last two steps, appropriately modified, for \({\bf Z}_y\) and \({\bf U}_y\) respectively.
The \({\bf I}\) Update
The first step of ADMM is to update \({\bf I}\). This is a straightforward \(L_2\) problem since the only terms that \({\bf I}\) appears is in terms with a 2-norm. Denoting \(\frac{\partial}{\partial x}{\bf I}\) as \({\bf D}_x \otimes {\bf I}\) and likewise for \(\frac{\partial}{\partial y}\), the solve ends up being:
\begin{equation*}
{\bf I} = \mbox{argmin} \frac{1}{2} \| {\bf K} \otimes {\bf I} - {\bf B} \|_2^2 + \frac{\rho}{2} \| {\bf D}_x \otimes {\bf I} - {\bf Z}_x + {\bf U}_x \|_2^2 + \frac{\rho}{2} \| {\bf D}_y \otimes {\bf I} - {\bf Z}_y + {\bf U}_y \|_2^2
\end{equation*}
All the terms are effectively the same: a minimization over the residual of a kernel convolved the the target image with respect to a measured value. The minimum is found by expanding out the term and finding the target image that sets the gradient of the expanded term to zero.
The solution for the first term in the Fourier domain is earlier in the post as:
\begin{equation*}
{\bf I} = \mathcal{F}^{-1}\left[ \frac{\mathcal{F}({\bf K})^*\mathcal{F}(\bf B)}{\mathcal{F}({\bf K})^2} \right]
\end{equation*}
The remaining terms follow the same pattern and sum in the numerator and denominator of the solve:
\begin{equation*}
{\bf I} = \mathcal{F}^{-1}\left[ \frac{
\mathcal{F}({\bf K})^*\mathcal{F}(\bf B)
+\rho \mathcal{F}({\bf D}_x)^*\mathcal{F}({\bf Z}_x - {\bf U}_x)
+\rho \mathcal{F}({\bf D}_y)^*\mathcal{F}({\bf Z}_y - {\bf U}_y)
}{\mathcal{F}({\bf K})^2 + \rho \mathcal{F}({\bf D}_x)^2 + \rho \mathcal{F}({\bf D}_y)^2} \right]
\end{equation*}
This involves 9 Fourier transforms, but only the terms containing \({\bf Z}_x,{\bf U}_x\) actually change during the solve (similarly for the y subscripts). By caching the first term of the numerator, the entire denominator, as well as \(\mathcal{F}({\bf D}_x)\mbox{ & }\mathcal{F}({\bf D}_y)\) this can be reduced to three transforms. It can further be reduced by evaluating the derivative filters \({\bf D}_x\mbox{ & }{\bf D}_y\) in the spatial domain, since they are very inexpensive finite difference filters. The following gets the \({\bf I}\) update down to one forward and one inverse transform once contants are cached:
\begin{align*}
{\bf V} = \rho \left( {\bf D}^T_x \otimes ({\bf Z}_x - {\bf U}_x) + {\bf D}^T_y \otimes ({\bf Z}_y - {\bf U}_y)\right) \\
{\bf I} = \mathcal{F}^{-1}\left[ \frac{
\mathcal{F}({\bf K})^*\mathcal{F}(\bf B) + \mathcal{F}({\bf V})
}{\mathcal{F}({\bf K})^2 + \rho \mathcal{F}({\bf D}_x)^2 + \rho \mathcal{F}({\bf D}_y)^2} \right]
\end{align*}
Important note: the \({\bf D}^T_x \otimes\) terms in \({\bf V}\) use the transposed filters (mixing notation terribly). This is the complex conjugate of the filter in the Fourier domain version, or matrix transpose if the convolution operation were represented in matrix form. Expressed as spatial domain convolution, the transpose simply requires mirroring the kernels horizontally and vertically about the central pixel.
The \({\bf Z}\) Updates
The next step of ADMM is to update the splitting variable \({\bf Z}_x\mbox{ & }{\bf Z}_y\). These terms only appear in one coupling terms and one \(L_1\) term each. The updates for the two \({\bf Z}\) and two \({\bf U}\) variables are the same except the specific filter that is used, so I'll only cover one. Here's the update needed for \({\bf Z}_x\):
\begin{equation*}
{\bf Z}_x = \mbox{argmin}_{{\bf Z}_x} \frac{\rho}{2} \| {\bf D}_x \otimes {\bf I} - {\bf Z}_x + {\bf U}_x \|_2^2 + \gamma \| {\bf Z}_x \|_1
\end{equation*}
It's important to note that there are no operators applied to \({\bf Z}_x\), meaning that each pixel can be processed independently. The terms can be rearranged and the weight factors collected onto the \(L_1\) term to give the equivalent minimization:
\begin{equation*}
{\bf Z}_x = \mbox{argmin}_{{\bf Z}_x} \frac{\gamma}{\rho} \| {\bf Z}_x \|_1 + \frac{1}{2} \| {\bf Z}_x - ({\bf D}_x \otimes {\bf I} + {\bf U}_x ) \|_2^2
\end{equation*}
However, a complication is (still) the \(L_1\) term. This is non-smooth and tricky to deal with but the form above allows a non-smooth optimization method known as proximal operators to be used. The proximal operator of a scaled function \(\lambda f(q)\) is defined as:
\begin{equation*}
\mbox{prox}_{\lambda f}({\bf q}) = \mbox{argmin}_{\bf p} f({\bf p}) + \frac{1}{2\lambda} \| {\bf p} - {\bf q} \|_2^2
\end{equation*}
The similarities with the \({\bf Z}_x\) minimization are strong. By setting \(f({\bf Z}_x)=\|{\bf Z}_x\|_1\mbox{ & }\lambda = \frac{\gamma}{\rho}\mbox{ & }{\bf q} = {\bf D}_x \otimes {\bf I} + {\bf U}_x\) the proximal operator is recovered. This is great because the closed form solution for \(\mbox{prox}_{\lambda\|{\bf p}\|_1}(\bf{q})\) is known and trivial to implement:
\begin{equation*}
\mbox{prox}_{\lambda\|{\bf p}\|_1}({\bf q}) = \mbox{sign}({\bf q}) \mbox{max}( 0, |{\bf q}| - \lambda)
\end{equation*}
This is known as the soft-thresholding operator, or \(L_1\) shrinkage operator and is used everywhere. It can be implemented in python as:
def soft_threshold( q, lam ):
return numpy.sign(q)*numpy.maximum( numpy.abs(q) - lam, 0.0 )
In my view, it's the most potent line of code that exists in signal processing.
The \({\bf U}\) Updates
The \({\bf U}\) updates simply add the current constraint violation to the Lagrange multipliers \({\bf U}\). It's kind of like the integral term in a PID controller.
The update was actually given already in the overview above but is repeated here for completeness:
\begin{align*}
{\bf U}_x = {\bf U}_x + {\bf D}_x \otimes {\bf I} - {\bf Z}_x \\
{\bf U}_y = {\bf U}_y + {\bf D}_x \otimes {\bf I} - {\bf Z}_y
\end{align*}
This is identical to the formula ealier, I've just used the \({\bf D}_x \otimes {\bf I}\) notation rather than \(\frac{\partial}{\partial x} {\bf I}\).
Summary
That's all the math that's needed. It looks like a lot but ends up being surprisingly little code. In the next part I work through the implementation.
In image reconstruction tasks, it's often convenient to perform filtering operations in either the spatial or frequency domain. Both have their advantages and disadvantages. For the spatial domain, small filters such as finite differences can be evaluated extremely quickly and include local coefficients but objective functions often result in large systems of equations. In contrast, many objective functions diagonalize to yield pixel-wise solutions in the frequency domain but spatial variation cannot be incorporated directly.
As a result, it's common to express reconstruction tasks with individual terms in each domain. The domains are then coupled through penalties or constraints that can be expressed naturally either domain and lead to efficient solvers.
By way of example: in the total-variation regularized inpainting example below, the data term expresses a least-squares penalty on a (fixed) random selection of pixels in the reconstruction \({\bf I}\) and measurements \({\bf Y}\) via the selection mask \({\bf S}\) (\(\odot\) is pixelwise multiplication). This term cannot be expressed efficiently in the Fourier domain. However the regularizers (e.g. \(\lambda \| \frac{\partial}{\partial x} {\bf I} \|_1\)) can and should be since otherwise they couple every pixel in the image together. This is bad because it results in very costly solves.
\begin{equation*}
{\bf I} = \mbox{argmin}_{\bf I} \frac{1}{2} \| S \odot \left( {\bf I} - {\bf Y} \right) \|_2^2
+ \lambda \| \frac{\partial}{\partial x} {\bf I} \|_1 + + \lambda \| \frac{\partial}{\partial y} {\bf I} \|_1
\end{equation*}
Solving this efficiently requires splitting the problem into separate solve that couple through constraints and Lagrange multipliers (or more simply through penalties). How to do that is an entire topic in itself but the key thing is that filtering is performed in both domains and must be consistent to produce sensible results. If this is not the case, all sorts of weird things happen: images shifting each iteration, convergence stalling, etc.
This sounds (and is) easy but requires a bit of attention to detail.
Brass Tacks
The starting point here is a definition of a sparse kernel. By sparse, I mean a kernel with very few non-zero weights, generally less than 10-20 or so. This includes common filters like Laplacians, edge filters and finite difference stencils.
In the following code, a kernel is defined by three equal length lists containing the row-offsets, column-offsets and filter values for the kernel. In the code, the user specifies the correlation kernel; this produces results that match typical finite-difference kernels when the correlate_spatial or correlate_fourier methods are called. Here is the code for the kernel class:
import numpy
class SparseKernel2D:
"""Represents a kernel for a 2D convolution operation
Example:
# make a first-order finite difference along the column axis
K = SparseKernel2D( [0,0], [-1,0], [-1.0, 1.0] )
"""
def __init__( self, offy, offx, vals ):
"""Represents a kernel for a 2D convolution operation
Args:
offy (integer array/list) vertical offsets of non-zero kernel values
offx (integer array/list) horizontal offsets of non-zero kernel values
vals (float array/list) non-zero kernel values
Raises:
ValueError whenever offx, offx, vals do not have the same length
"""
if len(offy) != len(offx) or len(vals) != len(offx):
raise ValueError('offx, offy and vals must be 1D array-like with the same size')
self.offx = offx
self.offy = offy
self.vals = vals
def image( self, dim ):
"""Returns an image represenation of the kernel at the specified dimensions with the kernel centered.
Args:
dim (integer tuple) output image dimensions [height,width]
Raises:
ValueError when dim is not 2-element
Returns:
height x width image of float32 elements
"""
if len(dim) != 2:
raise ValueError('Expected a 2-element integer tuple/list for image dimensions')
cen = ( int(dim[0]/2), int(dim[1]/2) )
out = numpy.zeros( dim, dtype=numpy.float32 )
for dx,dy,val in zip( self.offx, self.offy, self.vals):
out[cen[0]+dy,cen[1]+dx] = val
return out
def spectrum( self, dim ):
"""Returns a spectrum representation of the kernel at the specified dimensions. The returned
kernel is *not* centered, i.e. has it's DC component at the corner.
Args:
dim (integer tuple) output spectrum dimensions [height,width]
Raises:
ValueError when dim is not 2-element
Returns:
height x width complex image
"""
return numpy.fft.fft2( numpy.roll( self.image(dim), [int(dim[0]/2+0.5),int(dim[1]/2+0.5)], axis=[0,1] ) )
def convolve_spatial( self, I ):
"""Convolves the input image by the kernel in the spatial domain
Args:
I (2d float32 array) input image to convolve with kernel
Raises:
ValueError when input is not a 2D ndarray or I.dtype is not numpy.floating subclass
Returns:
Convolution results as 2D ndarray of I.dtype elements
"""
if not isinstance(I,numpy.ndarray) or I.ndim != 2 or not numpy.issubdtype(I.dtype,numpy.floating):
raise ValueError('Expected a 2D ndarray or float32 values')
result = numpy.zeros( I.shape, dtype=I.dtype )
for dx,dy,val in zip(self.offx, self.offy, self.vals):
result += val*numpy.roll( I, [dy,dx], axis=[0,1] )
return result
def correlate_spatial( self, I ):
"""Correlates the input image with the kernel in the spatial domain
"""
if not isinstance(I,numpy.ndarray) or I.ndim != 2 or not numpy.issubdtype(I.dtype,numpy.floating):
raise ValueError('Expected a 2D ndarray or float32 values')
result = numpy.zeros( I.shape, dtype=I.dtype )
for dx,dy,val in zip(self.offx, self.offy, self.vals):
result += val*numpy.roll( I, [-dy,-dx], axis=[0,1] )
return result
def convolve_fourier( self, I ):
"""Convolves the input image by the kernel in the Fourier domain
Args:
I (2d float32 array) input image to convolve with kernel
Raises:
ValueError when input is not a 2D ndarray or I.dtype is not numpy.floating subclass
Returns:
Convolution results as 2D ndarray of I.dtype elements
"""
if not isinstance(I,numpy.ndarray) or I.ndim != 2 or not numpy.issubdtype(I.dtype,numpy.floating):
raise ValueError('Expected a 2D ndarray or float32 values')
fK = self.spectrum( I.shape )
fI = numpy.fft.fft2( I )
return numpy.real( numpy.fft.ifft2( fK*fI ) )
def correlate_fourier( self, I ):
"""Correlates the input image by the kernel in the Fourier domain
Args:
I (2d float32 array) input image to convolve with kernel
Raises:
ValueError when input is not a 2D ndarray or I.dtype is not numpy.floating subclass
Returns:
Convolution results as 2D ndarray of I.dtype elements
"""
if not isinstance(I,numpy.ndarray) or I.ndim != 2 or not numpy.issubdtype(I.dtype,numpy.floating):
raise ValueError('Expected a 2D ndarray or float32 values')
fK = self.spectrum( I.shape )
fI = numpy.fft.fft2( I )
return numpy.real( numpy.fft.ifft2( numpy.conj(fK)*fI ) )
Testing & Validation
To ensure that indexing is done correctly, it's important to check that the kernel can represent an identity operation correctly for odd and even image sizes in both Fourier and spatial domains. After that, it's important that the convolution and correlation functions return the correct results.
This last point depends on whether the convolution or correlation filter is being defined. The difference between the two is mirroring horizontally and vertically. Personally, I find it most natural to define the correlation filter which coincides with the typical finite difference stencils. Generating some analytic data as well as some known finite difference kernels allows correct operation to be confirmed:
def TestSparseKernel2D():
"""Runs a series of test functions on the SparseKernel2D class"""
# local helper function that will raise an error if the
# results are insufficiently accurate
def MSE( x, ref ):
val = numpy.mean( numpy.power( x-ref, 2 ) )
if val > 1e-6:
raise ValueError('Values do not match!')
return val
# define a mean-squared error function
#MSE = lambda I, Ref: numpy.mean( numpy.power( I-Ref, 2 ) )
# generate an identity kernel
ident = SparseKernel2D( [0],[0],[1.0] )
# generate some test images
x,y = numpy.meshgrid( numpy.arange(0.,200.), numpy.arange(0.,100.) )
z = x+y
# check that convolving with the identity kernel
# reproduces the input for even mesh sizes
conv_z_s = ident.convolve_spatial( z )
conv_z_f = ident.convolve_fourier( z )
print('Identity test, even sizes: ',z.shape)
print('\tMSE spatial: %f'%MSE(conv_z_s,z) )
print('\tMSE fourier: %f'%MSE(conv_z_f,z) )
# check that convolving with the identity kernel
# reproduces the input for odd/even mesh sizes
tz = z[1:,:]
conv_z_s = ident.convolve_spatial( tz )
conv_z_f = ident.convolve_fourier( tz )
print('Identity test, odd/even sizes: ',tz.shape)
print('\tMSE spatial: %f'%MSE(conv_z_s,tz) )
print('\tMSE fourier: %f'%MSE(conv_z_f,tz) )
# check that convolving with the identity kernel
# reproduces the input for odd/even mesh sizes
tz = z[:,1:]
conv_z_s = ident.convolve_spatial( tz )
conv_z_f = ident.convolve_fourier( tz )
print('Identity test, even/odd sizes: ',tz.shape)
print('\tMSE spatial: %f'%MSE(conv_z_s,tz) )
print('\tMSE fourier: %f'%MSE(conv_z_f,tz) )
# check that convolving with the identity kernel
# reproduces the input for odd/odd mesh sizes
tz = z[:-1,1:]
conv_z_s = ident.convolve_spatial( tz )
conv_z_f = ident.convolve_fourier( tz )
print('Identity test, odd/odd sizes: ',tz.shape)
print('\tMSE spatial: %f'%MSE(conv_z_s,tz) )
print('\tMSE fourier: %f'%MSE(conv_z_f,tz) )
# generate first order finite difference formula
# try convolving in both the spatial and frequency
# domains
ddx = SparseKernel2D( [0,0],[-1,0],[-1.0,1.0] )
ddx_z_s = ddx.correlate_spatial( z )[1:-2,1:-2]
ddx_z_f = ddx.correlate_fourier( z )[1:-2,1:-2]
ones = numpy.ones( ddx_z_s.shape, dtype=numpy.float32 )
print('First order finite-difference d(x+y)/dx')
print('\tMSE spatial: %f' % MSE(ddx_z_s,ones) )
print('\tMSE fourier: %f' % MSE(ddx_z_f,ones) )
# generate first order finite difference formula
# try convolving in both the spatial and frequency
# domains
ddy = SparseKernel2D( [-1,0],[0,0],[-1.0,1.0] )
ddy_z_s = ddy.correlate_spatial( z )[1:-2,1:-2]
ddy_z_f = ddy.correlate_fourier( z )[1:-2,1:-2]
ones = numpy.ones( ddy_z_s.shape, dtype=numpy.float32 )
print('First order finite-difference d(x+y)/dy')
print('\tMSE spatial: %f' % MSE(ddy_z_s,ones) )
print('\tMSE fourier: %f' % MSE(ddy_z_f,ones) )
# now try the convolution functions, this simply
# flips the kernel about the central pixel
# horizontally and vertically. for the filters
# defined above, this negates the results
ddx_z_s = ddx.convolve_spatial( z )[1:-2,1:-2]
ddx_z_f = ddx.convolve_fourier( z )[1:-2,1:-2]
ones = numpy.ones( ddx_z_s.shape, dtype=numpy.float32 )
print('Convolved first order finite-difference d(x+y)/dx')
print('\tMSE spatial: %f' % MSE(ddx_z_s,-ones) )
print('\tMSE fourier: %f' % MSE(ddx_z_f,-ones) )
# generate first order finite difference formula
# try convolving in both the spatial and frequency
# domains
ddy_z_s = ddy.convolve_spatial( z )[1:-2,1:-2]
ddy_z_f = ddy.convolve_fourier( z )[1:-2,1:-2]
ones = numpy.ones( ddy_z_s.shape, dtype=numpy.float32 )
print('Convolved first order finite-difference d(x+y)/dy')
print('\tMSE spatial: %f' % MSE(ddy_z_s,-ones) )
print('\tMSE fourier: %f' % MSE(ddy_z_f,-ones) )
This prints:
Identity test, even sizes: (100, 200)
MSE spatial: 0.000000
MSE fourier: 0.000000
Identity test, odd/even sizes: (99, 200)
MSE spatial: 0.000000
MSE fourier: 0.000000
Identity test, even/odd sizes: (100, 199)
MSE spatial: 0.000000
MSE fourier: 0.000000
Identity test, odd/odd sizes: (99, 199)
MSE spatial: 0.000000
MSE fourier: 0.000000
First order finite-difference d(x+y)/dx
MSE spatial: 0.000000
MSE fourier: 0.000000
First order finite-difference d(x+y)/dy
MSE spatial: 0.000000
MSE fourier: 0.000000
Convolved first order finite-difference d(x+y)/dx
MSE spatial: 0.000000
MSE fourier: 0.000000
Convolved first order finite-difference d(x+y)/dy
MSE spatial: 0.000000
MSE fourier: 0.000000

