Jul 22, 2023
This came up years ago for me as an interview question that I flubbed badly. The task was to write a simplified regular expression matching algorithm that would test if a given string matched the provided pattern. The set of valid patterns was considerably simplified from full regular expressions to be only matching single characters or the Kleene Star * which matched zero or more instances of the previous character.
I quickly put together an implementation that worked well greedily but stumbled on backtracking, which is needed to match patterns like "aa*a". This should match strings "aa", "aaa", aaaa", and so on. However, to match the final character it is necessary to not consume the final "a" with the Kleene star since this would exhaust the input before reaching the final term. I was not able to figure out how to do this and did not get the job.
Now I do know how to do this. This post documents how not just for the simple case above but also a much more complete set of patterns.
Preamble
In the end, the bit I was missing was backtracking. As the pattern is matched, the matching algorithm needs to track a state indicating both where it is in the input and where it is in the pattern. In greedy matching, only a single state is maintained and the match fails whenever the next term fails to match or the input is exhausted before reachind the end of the pattern. The latter is what happens in the example at the start, the "a*"" term gobbles up all the input "a"s leaving the final a in the pattern unmatched.
For a backtracking implmentation, the algorithm creates & tracks a set of states, each corresponding to one of several discrete choices that can be made during the algorithm. These states are advanced as input is parsed and the match fails when all of the states fail to match.
In the simple expression grammar above, the discrete choices are to either match or skip matching an additional "a" when (recursively) handling the Kleene Star.
So a backtracking algorithm needs to be able to keep track of multiple states, each indicating the input position and pattern position, advance each state through the input and cull those states whenever they fail to match. If any state reaches the end of the pattern, the string matches.
Pattern Representation
The matching algorithm I'll describe here is richer than the introductory example. It supports matching any specified character, a binary or '|' operator that matches either the left or right operand, a binary and '&' operator that matches both the left & right operand in order and the Kleene Star '*'. The first is a terminal node of the expression tree, while the '&', '|' and '*' operators are internal nodes.
In addition, a nop node '~' is another terminal that automatically matches but consumes no input. It is helpful for defining other operations, e.g. "a?" matches zero or one instances of character "a" and can be defined as "~|a". It also ensures that every non-terminal node has both left and right children.
Beyond this, there are number of other node types that are pretty easy to figure out once the above are handled.
To represent this, an array-based tree is used with each element containing the following structure:
struct node_t {
constexpr static int INVALID = -1;
int parent = INVALID;
int left = INVALID;
int right = INVALID;
type_t type = type_t::NOP;
int data = -1;
};
Parent, left and right are indices of the corresponding nodes in the array and are used to walk the tree when matching. node_t::INVALID is used to represent the parent of the root node. The data field is used by the character node to define what character to match in the input while the type indicates the type of node as defined below:
enum type_t { NOP, CHAR, ANY, END, AND, OR, STAR, PLUS };
State Representation
This is enough to define tree but it is still necessary to track the matching algorithm state. To perform the matching, the algorithm walks the tree down to the left most terminal. If the terminals matches, it walks back up to the terminal's parent. Depending on the node type, it then either evaluates the right child or walks up to it's parent.
The algorithm state representation used is the currently visited node and the node that it arrived from as well as the current position in the input. This is enough to know both where in the tree we are and where we came from, which is enough to know what needs to be evaluated next.
In this algorithm, these states are tracked via a matching stack:
// stack entries are {input_pos, current_node, previous_node}
using match_stack_t = std::stack<std::tuple<const char*,int,int>>;
Matching Algorithm via Tree Traversal
By knowing where we are in the input and where we are in the tree and how we got there, we can implement the matching recursively. However, it is not desireable to actually use recursion because we could end up exhausting the call stack on long inputs. Instead we use a stack as above (and potentially exhaust memory instead).
At each iteration, we will pull a state from the stack. First we will check if we've exhausted the input string. If so the current state is culled. Then we will check if we've successfully processed the root node after recursing back up the tree. If so and input was consumed from the string, we've successfully matched the expression. Otherwise the state is culled.
result_t match( const char *input ) const {
match_stack_t stack;
const int n = strlen(input)+1;
// tree is built in post-fix order so root is last node
stack.push({input,int(_tree.size())-1,node_t::INVALID});
while( !stack.empty() ){
auto [str,node,last] = stack.top();
stack.pop();
if( str-input >= n ){
// exhausted input, consider remaining states
continue;
} else if( node == node_t::INVALID ){
// finished recursing back to root
if( str != input ){
// consumed input, successfully matched
return {true,str};
}
// did not consume input, match failed, try
// remaining states
continue;
}
switch( _tree[node].type ){
case type_t::NOP:
walk_nop( stack, str, node, last );
break;
case type_t::CHAR:
walk_char( stack, str, node, last );
break;
... other node types ...
case type_t::AND:
walk_and( stack, str, node, last );
break;
case type_t::OR:
walk_or( stack, str, node, last );
break;
case type_t::STAR:
walk_star( stack, str, node, last );
break;
... other node types ...
}
}
// exhausted regular expression or input
return {false,input};
}
Following this, we traverse the tree according to a set of rules for each node. The rules depend on the node type. The one common theme is that on a successful match at a subtree a new state is pushed with the input position and starting at the subtree's parent arriving from the subtree. However, when the subtree does not match, it does not push a new state and the state is culled.
For example, if we are at an '&' node and came from the '&' node's parent, we need to evaluate the left subtree. If we arrived from the left subtree, we need to evaluate the right subtree. Finally if we arrived from the right subtree, we need to go back up to the '&' node's parent.
void walk_and( match_stack_t& stack, const char* str, int node, int last ) const {
if( last == node_t::INVALID || last == _tree[node].parent ){
stack.push({str,_tree[node].left,node});
} else if( last == _tree[node].left ){
stack.push({str,_tree[node].right,node});
} else if( last == _tree[node].right ){
stack.push({str,_tree[node].parent,node});
} else {
assert( false && "Should never happen. Tree is borked!");
}
}
If, however, we are at an '|' node we first check the left subtree. If it matches, we recurse back up to the '|' node's parent and skip checking the right operand. This is done by pushing both left and right nodes onto the stack at the current position, if the left traveral fails, the algorithm will pop the right state and proceed from there. If we sucessfully arrive back at the '|' node from either of the subtrees, the match succeeded and we head back up to the parent node:
void walk_or( match_stack_t& stack, const char* str, int node, int last ) const {
if( last == node_t::INVALID || last == _tree[node].parent ){
stack.push({str,_tree[node].right,node});
stack.push({str,_tree[node].left, node});
} else if( last == _tree[node].left || last == _tree[node].right ){
stack.push({str,_tree[node].parent,node});
} else {
assert( false && "Should never happen. Tree is borked!");
}
}
The Kleene Star is similar to the '|' case except whenever we arrive at the '*' node we push both its parent and its left subtree. The order these are pushed determines whethe the '*' is greedy (tries to consume as much input as possible) or non-greedy (tries to consume as little as possible). This is the greedy version since it will retry the left subtree before recursing back to the parent.
void walk_star( match_stack_t& stack, const char* str, int node, int last ) const {
if( last == node_t::INVALID || last == _tree[node].parent ){
stack.push({str,_tree[node].parent, node});
stack.push({str,_tree[node].left, node});
} else if( last == _tree[node].left ){
stack.push({str,_tree[node].parent,node});
stack.push({str,_tree[node].left, node});
} else {
assert( false && "Should never happen. Tree is borked!");
}
}
Finally to pull it all together, there need to be the correponding implmentations for the '~' and character terminals. In the case of the nop, the string position remains the same and we move back to the parent node. The character node is almost the same, except we only recurse back if the next input character matches. In that case, we advance the string and recurse back to the parent node. Otherwise, the match for this state does not continue. These are:
void walk_nop( match_stack_t& stack, const char* str, int node, int last ) const {
stack.push({str,last,node});
}
void walk_char( match_stack_t& stack, const char* str, int node, int last ) const {
if( *str == _tree[node].data ){
stack.push({str+1,last,node});
}
}
Aside from some boilerplate to actually build the tree, the definition of the result type and a class to wrap it all together, that's really all there is to it.
The full example, including additional node types, is below
Full Example Source Code
#include <string>
#include <cassert>
#include <iostream>
#include <stack>
#include <tuple>
#include <vector>
class regex_t {
public:
struct result_t {
bool result;
const char* remainder;
operator bool() const { return result; }
operator const char*() const { return remainder; }
};
result_t match( const char *input ) const {
match_stack_t stack;
const int n = strlen(input)+1;
// tree is built in post-fix order so root is last node
stack.push({input,int(_tree.size())-1,node_t::INVALID});
while( !stack.empty() ){
auto [str,node,last] = stack.top();
stack.pop();
if( str-input >= n ){
// exhausted input, consider remaining states
continue;
} else if( node == node_t::INVALID ){
// finished recursing back to root
if( str != input ){
// consumed input, successfully matched
return {true,str};
}
// did not consume input, match failed, try
// remaining states
continue;
}
switch( _tree[node].type ){
case type_t::NOP:
walk_nop( stack, str, node, last );
break;
case type_t::CHAR:
walk_char( stack, str, node, last );
break;
case type_t::ANY:
walk_any( stack, str, node, last );
break;
case type_t::END:
walk_end( stack, str, node, last );
break;
case type_t::AND:
walk_and( stack, str, node, last );
break;
case type_t::OR:
walk_or( stack, str, node, last );
break;
case type_t::STAR:
walk_star( stack, str, node, last );
break;
case type_t::PLUS:
walk_plus( stack, str, node, last );
break;
}
}
// exhausted regular expression or input
return {false,input};
}
int nop(){
return add_terminal( {.type=type_t::NOP} );
}
int character( const char match ){
assert( match > 0 );
return add_terminal( {.type = type_t::CHAR, .data = match} );
}
int any(){
return add_terminal( {.type = type_t::ANY } );
}
int end(){
return add_terminal( {.type = type_t::END} );
}
int both( const int left, const int right ){
return add_tree( {.type = type_t::AND}, left, right );
}
int either( const int left, const int right ){
return add_tree( {.type = type_t::OR}, left, right );
}
int star( const int left ){
return add_tree( {.type = type_t::STAR}, left, nop() );
}
int plus( const int left ){
return add_tree( {.type = type_t::PLUS}, left, nop() );
}
int maybe( const int left ){
return either( left, nop() );
}
private:
using match_stack_t = std::stack<std::tuple<const char*,int,int>>;
enum type_t { NOP, CHAR, ANY, END, AND, OR, STAR, PLUS };
struct node_t {
constexpr static int INVALID = -1;
int parent = INVALID;
int left = INVALID;
int right = INVALID;
type_t type = type_t::NOP;
int data = -1;
};
void walk_nop( match_stack_t& stack, const char* str, int node, int last ) const {
stack.push({str,last,node});
}
void walk_char( match_stack_t& stack, const char* str, int node, int last ) const {
if( *str == _tree[node].data ){
stack.push({str+1,last,node});
}
}
void walk_any( match_stack_t& stack, const char* str, int node, int last ) const {
if( *str != '\0' ){
stack.push({str+1,last,node});
}
}
void walk_end( match_stack_t& stack, const char* str, int node, int last ) const {
if( *str == '\0' ){
stack.push({str,last,node});
}
}
void walk_and( match_stack_t& stack, const char* str, int node, int last ) const {
if( last == node_t::INVALID || last == _tree[node].parent ){
stack.push({str,_tree[node].left,node});
} else if( last == _tree[node].left ){
stack.push({str,_tree[node].right,node});
} else if( last == _tree[node].right ){
stack.push({str,_tree[node].parent,node});
} else {
assert( false && "Should never happen. Tree is borked!");
}
}
void walk_or( match_stack_t& stack, const char* str, int node, int last ) const {
if( last == node_t::INVALID || last == _tree[node].parent ){
stack.push({str,_tree[node].right,node});
stack.push({str,_tree[node].left, node});
} else if( last == _tree[node].left || last == _tree[node].right ){
stack.push({str,_tree[node].parent,node});
} else {
assert( false && "Should never happen. Tree is borked!");
}
}
void walk_star( match_stack_t& stack, const char* str, int node, int last ) const {
if( last == node_t::INVALID || last == _tree[node].parent ){
stack.push({str,_tree[node].parent, node});
stack.push({str,_tree[node].left, node});
} else if( last == _tree[node].left ){
stack.push({str,_tree[node].parent,node});
stack.push({str,_tree[node].left, node});
} else {
assert( false && "Should never happen. Tree is borked!");
}
}
void walk_plus( match_stack_t& stack, const char* str, int node, int last ) const {
if( last == node_t::INVALID || last == _tree[node].parent ){
stack.push({str,_tree[node].left, node});
} else if( last == _tree[node].left ){
stack.push({str,_tree[node].parent,node});
stack.push({str,_tree[node].left, node});
} else {
assert( false && "Should never happen. Tree is borked!");
}
}
// builder stuff
int add_terminal( const node_t& n ){
_tree.emplace_back( n );
return _tree.size()-1;
}
int add_tree( const node_t& n, int left, int right ){
assert( left >= 0 && left < _tree.size() && right >= 0 && right < _tree.size() );
int parent = add_terminal( n );
_tree[parent].left = left;
_tree[parent].right = right;
_tree[ left].parent = parent;
_tree[right].parent = parent;
return parent;
}
std::vector<node_t> _tree;
};
std::ostream& operator<<( std::ostream& os, const regex_t::result_t& res ){
os << (res.result ? "match succeeded" : "match_failed") << ", remainder: \"" << res.remainder << "\"" << std::endl;
return os;
}
int main( int argc, char **argv ){
regex_t re;
re.both(
re.character('a'),
re.both(
re.plus(
re.character('a')
),
re.both(
re.character('a'),
re.end()
)
)
);
std::cout << re.match("aaa") << std::endl;
return 0;
}
Apr 09, 2023
This was mildly fiddly so I'm putting information here.
First set your home router to pass ports 80 and 443 to the target machine. Verify that you have done this successfully by trying to connect from a machine that is outside your LAN, e.g. a mobile phone using cell rather than wifi, to your (current) public IP. To do this, I use Python's built-in http server:
cat 'hello world' > index.html
python3 -m http.server
Connect to your IP from outside your LAN and you should see hello world in your browers. Assuming that was successful and that your server is a Ubuntu/Debian-based machine, install ddclient:
sudo apt install ddclient
It will guide you through setup but for me it did not work. You might be tempted to use the google domains option but this did not work for me. Try it anyway and if/when it fails use something like the following. Do not include http:// or https:// in the <your domain> portion.
protocol=dyndns2
use=web
server=domains.google.com
ssl=yes
login='<google-generated-login>'
password='<google-generated-password>'
<your domain>
The login and password fields are not your Google account username and password. They are generated by Google. Open your domain in Google domains and go to the DNS section, then scroll down to and enable Show Advanced Settings and then expnd the Dynamic DNS collapsed panel. Then click View Credentials (red arrow below) and you should see the following. You can get your login/password by clicking View on the panel that pops up.
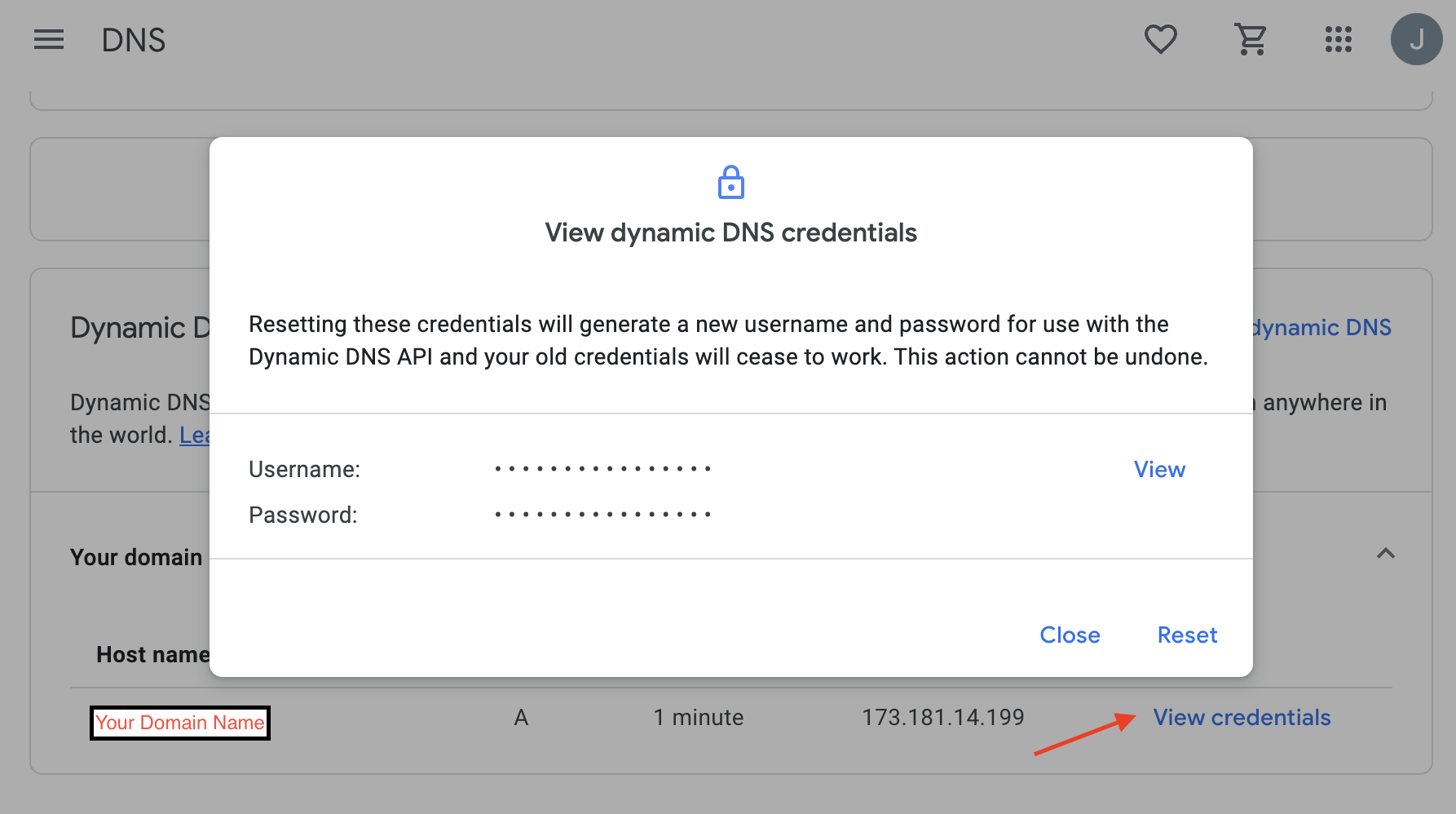
You can then run:
sudo service ddclient restart
to restart ddclient and run:
sudo ddclient query
to perform an update. Refreshing the google domains page for the domain should ideally show that the record has been updated. Using your external-to-your-LAN-machine, you should now
Jun 09, 2022
Given two matrices \(A \in \mathcal{R}^{M\times S}\) and \(B \in \mathcal{R}^{S \times N}\) it is helpful to be able to reorder their product \(A B \in \mathcal{R}^{M\times N}\) in order to compute Jacobians for optimization. For this it is common to define the \(\mbox{vec}(.)\) operator which flattens a matrix into a vector by concatenating columns:
\begin{equation*}
\newcommand{\vec}[1]{\mbox{vec}{\left(#1\right)}}
\vec{A} = \begin{bmatrix} A_{11} \\ \vdots \\ A_{M1} \\ \vdots \\ A_{1S} \\ \vdots \\ A_{MS}\end{bmatrix}
\end{equation*}
Using this operator, the (flattened) product \(AB\) can be written as one of:
\begin{align*}
\vec{AB} &=& (B^T \otimes I_A)\vec{A} \\
&=& (I_B \otimes A)\vec{B}
\end{align*}
where \(\otimes\) is the Kronecker Product and \(I_A\) is an identity matrix with the same number of rows as \(A\) and \(I_B\) is an idenity matrix with the same number of columns as \(B\).
From the two options for expressing the product, it's clear that \((B^T \otimes I_A)\) is the (vectorized) Jacobian of \(AB\) with respect to \(A\) and \((I_B \otimes A)\) is the corresponding vectorized Jacobian with respect to \(B\).
That's great but if our linear algebra library happens to represent matrices in row-major order it will be necessary to sprinkle a large number of transposes in to get things in the right order to apply these formulas. That will be tedious, error-prone and inefficient. Fortunately, equivalent formulas are available for row-major ordering by defining a \(\mbox{ver}(.)\) operator that flattens a matrix by concatenating rows to form a column vector:
\begin{equation*}
\newcommand{\ver}[1]{\mbox{ver}{(#1)}}
\ver{A} = \begin{bmatrix} A_{11} \\ \vdots \\ A_{1S} \\ \vdots \\ A_{M1} \\ \vdots \\ A_{MS} \end{bmatrix}
\end{equation*}
Given this it is fairly quick to work out that the equivalent to the first two formulas using the \(\ver{.}\) operator are:
\begin{align*}
\ver{AB} &=& (I_A \otimes B^T)\ver{A} \\
&=& ( A \otimes I_B)\ver{B}
\end{align*}
Using the same logic it can be concluded that \((I_A \otimes B^T)\) is the vectorized Jacobian of \(AB\) with respect to \(A\) and \((A \otimes I_B)\) is the corresponding Jacobian with respect to \(B\).
It's also worth noting that these are simplifications of a more general case for the product \(AXB\) that brings \(X\) to the right of the expression. The corresponding \(\vec{.}\) and \(\ver{.}\) versions are:
\begin{align*}
\vec{AXB} &=& (B^T \otimes A) \vec{X} \\
\ver{AXB} &=& (A \otimes B^T) \ver{X}
\end{align*}
which makes it clear where the identity matrices \(I_A\) and \(I_B\) in the previous expressions originate.
All these can be demonstrated by the following python code sample:
from typing import Tuple
import numpy as np
def vec( M: np.ndarray ):
'''Flatten argument by columns'''
return M.flatten('F')
def ivec( v: np.ndarray, shape: Tuple[int,int] ):
'''Inverse of vec'''
return np.reshape( v, shape, 'F' )
def ver( M: np.ndarray ):
'''Flatten argument by rows'''
return M.flatten('C')
def iver( v: np.ndarray, shape: Tuple[int,int] ):
'''Inverse of ver'''
return np.reshape( v, shape, 'C' )
def test_vec_ivec():
A = np.random.standard_normal((3,4))
assert np.allclose( A, ivec( vec( A ), A.shape ) )
def test_ver_iver():
A = np.random.standard_normal((3,4))
assert np.allclose( A, iver( ver(A), A.shape ) )
def test_products():
A = np.random.standard_normal((3,4))
X = np.random.standard_normal((4,4))
B = np.random.standard_normal((4,5))
AB1 = A@B
Ia = np.eye( A.shape[0] )
Ib = np.eye( B.shape[1] )
AB2a = ivec( np.kron( B.T, Ia )@vec(A), (A.shape[0],B.shape[1]) )
AB2b = ivec( np.kron( Ib, A )@vec(B), (A.shape[0],B.shape[1]) )
assert np.allclose( AB1, AB2a )
assert np.allclose( AB1, AB2b )
AB3a = iver( np.kron( A, Ib )@ver(B), (A.shape[0], B.shape[1]) )
AB3b = iver( np.kron( Ia, B.T )@ver(A), (A.shape[0], B.shape[1]) )
assert np.allclose( AB1, AB3a )
assert np.allclose( AB1, AB3b )
AXB1 = A@X@B
AXB2 = ivec( np.kron(B.T,A)@vec(X), (A.shape[0],B.shape[1]) )
AXB3 = iver( np.kron(A,B.T)@ver(X), (A.shape[0],B.shape[1]) )
assert np.allclose( AXB1, AXB2 )
assert np.allclose( AXB1, AXB3 )
if __name__ == '__main__':
test_vec_ivec()
test_ver_iver()
test_products()
Hopefully this is helpful to someone.
Jun 14, 2021
Given a linear model \(y_i = x_i^T \beta\), we collect \(N\) observations \(\tilde{y_i} = y_i + \epsilon_i\) where \(\epsilon_i \sim \mathcal{N}(0,\sigma^2)\). The likelihood of any one of our observations \(\tilde{y_i}\) given current estimates of our parameters \(\beta\) is then:
\begin{equation*}
\newcommand{\exp}[1]{{\mbox{exp}\left( #1 \right)}}
\newcommand{\log}[1]{{\mbox{log}\left( #1 \right)}}
\DeclareMathOperator*{\argmax}{argmax}
\DeclareMathOperator*{\argmin}{argmin}
P(\tilde{y}_i | \beta) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp{-\frac{1}{2}\left(\frac{e_i}{\sigma}\right)^2} = \frac{1}{\sqrt{2\pi\sigma^2}} \exp{-\frac{1}{2}\left(\frac{\tilde{y_i}-x_i^T \beta}{\sigma}\right)^2}
\end{equation*}
and the likelihood of all of them occuring is:
\begin{equation*}
P(\tilde{y} | \beta) = \prod_{i=1}^N P(\tilde{y}_i | \beta )
\end{equation*}
The parameters most likely to explain the observations, given only the observations and definition of the model, are those that maximize this likelihood. Equivalently, we can find the parameters that minimize the negative log-likelihood since the two have the same optima:
\begin{align*}
\beta^* &=& \argmax_\beta P(\tilde{y} | \beta) \\
&=& \argmin_\beta - \ln( P(\tilde{y} | \beta ) \\
&=& \argmin_\beta - N\log{\frac{1}{\sqrt{2\pi\sigma^2}}} - \log{ \prod_{i=1}^N P(\tilde{y}_i | \beta ) }
\end{align*}
The benefit of this is that the terms decouple in the case of normally distributed residuals. Ditching constant factors and collecting the product terms into the exponent the above becomes:
\begin{align*}
\beta^* &=& \argmin_\beta -\ln\left( \exp{-\frac{1}{2}\sum_{i=1}^N \left(\frac{\tilde{y}_i - M_i^T \beta}{\sigma}\right)^2} \right) \\
&=& \argmin_\beta \frac{1}{2\sigma^2} \sum_{i=1}^N \left( \tilde{y}_i - M_i^T \beta \right)^2
\end{align*}
which gives the least-squares version.
Least Squares & MAP
We can also add a prior for the parameters \(\beta\), e.g. \(\beta_i \sim \mathcal{N}(0,\sigma_\beta)\). In this case, each component of \(\beta\) is independent. The MAP estimate for \(\beta\) is then:
\begin{align*}
\beta^* &=& \argmax_\beta P(\tilde{y} | \beta) P(\beta) \\
&=& \argmax_\beta \prod_i P(\tilde{y}_i | \beta) \prod_j P(\beta_j) \\
&=& \argmax_\beta \prod_i \frac{1}{\sqrt{2\pi\sigma^2}}\exp{ -\frac{1}{2}\left(\frac{e_i}{\sigma}\right)^2} \prod_j \frac{1}{\sqrt{2\pi\sigma_\beta^2}}\exp{ -\frac{1}{2}\left(\frac{\beta_j}{\sigma_\beta}\right)^2 }
\end{align*}
The same negative log trick can then be used to convert products to sums, also ditching constants, to get:
\begin{align*}
\beta^* &=& \argmin \frac{1}{2\sigma^2} \sum_i e_i^2 + \frac{1}{2\sigma_\beta^2} \sum_j \beta_j^2 \\
&=& \argmin \frac{1}{2\sigma^2} \sum_i \left( \tilde{y}_i - x_i^T \beta \right)^2 + \frac{1}{2\sigma_\beta^2} \sum_j \beta_j^2
\end{align*}
Using different priors will of course give different forms for the second term, e.g. choosing components of \(\beta\) to follow a Laplace distribution \(\beta_j \sim \frac{\lambda}{2} \exp{-\lambda |\beta_j|}\), gives:
\begin{equation*}
\beta^* = \argmin \frac{1}{2\sigma^2} \sum_i \left( \tilde{y}_i - x_i^T \beta \right)^2 + \lambda \sum_j |\beta_j|
\end{equation*}
Dec 13, 2020
The essential matrix relates normalized coordinates in one view with those in another view of the same scene and is widely used in stereo reconstruction algorithms. It is a 3x3 matrix with rank 2, having only 8 degrees of freedom.
Given \(p\) as a normalized point in image P and \(q\) as the corresponding normalied point in another image Q of the same scene, the essential matrix provides the constraint:
\begin{equation*}
q^T E p = 0
\end{equation*}
It's important that \(p\) and \(q\) be normalized homogeneous points, i.e. the following where \([u_p,v_p]\) are the pixel coordinates of point p:
\begin{equation*}
p = K^{-1} \begin{bmatrix} u_p \\ v_p \\ 1 \end{bmatrix}
\end{equation*}
By fixing the extrinsics of image P as \(R_P = I\) and \(t_P = [0,0,0]^T\) the essential matrix relating P and Q can defined by the relationship:
\begin{equation*}
E = t_\times R
\end{equation*}
where \(R\) and \(t\) are the relative transforms of camera Q with respect to camera P and \(t_\times\) is the matrix representation of the the cross-product:
\begin{equation*}
t_\times = \begin{bmatrix} 0 & -t_z & t_y \\ t_z & 0 & -t_x \\ -t_y & t_x & 0 \end{bmatrix}
\end{equation*}
Nov 07, 2019
It's pretty useful to be able to load meshes when doing graphics. One format that is nearly ubiquitous are Wavefront .OBJ files, due largely to their good features-to-complexity ratio. Sure there are better formats, but when you just want to get a mesh into a program it's hard to beat .obj which can be imported and exported from just about anyhwere.
The code below loads and saves .obj files, including material assignments (but not material parameters), normals, texture coordinates and faces of any number of vertices. It supports faces with/without either/both of normals and texture coordinates and (if you can accept 6D vertices) also suports per-vertex colors (a non-standard extension sometimes used for debugging in mesh processing). Faces without either normals or tex-coords assign the invalid value -1 for these entries.
From the returned object, it is pretty easy to do things like sort faces by material indices, split vertices based on differing normals or along texture boundaries and so on. It also has the option to tesselate non-triangular faces, although this only works for convex faces (you should only be using convex faces anyway though!).
# wavefront.py
import numpy as np
class WavefrontOBJ:
def __init__( self, default_mtl='default_mtl' ):
self.path = None # path of loaded object
self.mtllibs = [] # .mtl files references via mtllib
self.mtls = [ default_mtl ] # materials referenced
self.mtlid = [] # indices into self.mtls for each polygon
self.vertices = [] # vertices as an Nx3 or Nx6 array (per vtx colors)
self.normals = [] # normals
self.texcoords = [] # texture coordinates
self.polygons = [] # M*Nv*3 array, Nv=# of vertices, stored as vid,tid,nid (-1 for N/A)
def load_obj( filename: str, default_mtl='default_mtl', triangulate=False ) -> WavefrontOBJ:
"""Reads a .obj file from disk and returns a WavefrontOBJ instance
Handles only very rudimentary reading and contains no error handling!
Does not handle:
- relative indexing
- subobjects or groups
- lines, splines, beziers, etc.
"""
# parses a vertex record as either vid, vid/tid, vid//nid or vid/tid/nid
# and returns a 3-tuple where unparsed values are replaced with -1
def parse_vertex( vstr ):
vals = vstr.split('/')
vid = int(vals[0])-1
tid = int(vals[1])-1 if len(vals) > 1 and vals[1] else -1
nid = int(vals[2])-1 if len(vals) > 2 else -1
return (vid,tid,nid)
with open( filename, 'r' ) as objf:
obj = WavefrontOBJ(default_mtl=default_mtl)
obj.path = filename
cur_mat = obj.mtls.index(default_mtl)
for line in objf:
toks = line.split()
if not toks:
continue
if toks[0] == 'v':
obj.vertices.append( [ float(v) for v in toks[1:]] )
elif toks[0] == 'vn':
obj.normals.append( [ float(v) for v in toks[1:]] )
elif toks[0] == 'vt':
obj.texcoords.append( [ float(v) for v in toks[1:]] )
elif toks[0] == 'f':
poly = [ parse_vertex(vstr) for vstr in toks[1:] ]
if triangulate:
for i in range(2,len(poly)):
obj.mtlid.append( cur_mat )
obj.polygons.append( (poly[0], poly[i-1], poly[i] ) )
else:
obj.mtlid.append(cur_mat)
obj.polygons.append( poly )
elif toks[0] == 'mtllib':
obj.mtllibs.append( toks[1] )
elif toks[0] == 'usemtl':
if toks[1] not in obj.mtls:
obj.mtls.append(toks[1])
cur_mat = obj.mtls.index( toks[1] )
return obj
def save_obj( obj: WavefrontOBJ, filename: str ):
"""Saves a WavefrontOBJ object to a file
Warning: Contains no error checking!
"""
with open( filename, 'w' ) as ofile:
for mlib in obj.mtllibs:
ofile.write('mtllib {}\n'.format(mlib))
for vtx in obj.vertices:
ofile.write('v '+' '.join(['{}'.format(v) for v in vtx])+'\n')
for tex in obj.texcoords:
ofile.write('vt '+' '.join(['{}'.format(vt) for vt in tex])+'\n')
for nrm in obj.normals:
ofile.write('vn '+' '.join(['{}'.format(vn) for vn in nrm])+'\n')
if not obj.mtlid:
obj.mtlid = [-1] * len(obj.polygons)
poly_idx = np.argsort( np.array( obj.mtlid ) )
cur_mat = -1
for pid in poly_idx:
if obj.mtlid[pid] != cur_mat:
cur_mat = obj.mtlid[pid]
ofile.write('usemtl {}\n'.format(obj.mtls[cur_mat]))
pstr = 'f '
for v in obj.polygons[pid]:
# UGLY!
vstr = '{}/{}/{} '.format(v[0]+1,v[1]+1 if v[1] >= 0 else 'X', v[2]+1 if v[2] >= 0 else 'X' )
vstr = vstr.replace('/X/','//').replace('/X ', ' ')
pstr += vstr
ofile.write( pstr+'\n')
A function that round-trips the loader is shown below, the resulting mesh dump.obj can be loaded into Blender and show the same material ids and texture coordinates. If you inspect it (and remove comments) you will see that the arrays match the string in the function:
from wavefront import *
def obj_load_save_example():
data = '''
# slightly edited blender cube
mtllib cube.mtl
v 1.000000 1.000000 -1.000000
v 1.000000 -1.000000 -1.000000
v 1.000000 1.000000 1.000000
v 1.000000 -1.000000 1.000000
v -1.000000 1.000000 -1.000000
v -1.000000 -1.000000 -1.000000
v -1.000000 1.000000 1.000000
v -1.000000 -1.000000 1.000000
vt 0.625000 0.500000
vt 0.875000 0.500000
vt 0.875000 0.750000
vt 0.625000 0.750000
vt 0.375000 0.000000
vt 0.625000 0.000000
vt 0.625000 0.250000
vt 0.375000 0.250000
vt 0.375000 0.250000
vt 0.625000 0.250000
vt 0.625000 0.500000
vt 0.375000 0.500000
vt 0.625000 0.750000
vt 0.375000 0.750000
vt 0.125000 0.500000
vt 0.375000 0.500000
vt 0.375000 0.750000
vt 0.125000 0.750000
vt 0.625000 1.000000
vt 0.375000 1.000000
vn 0.0000 0.0000 -1.0000
vn 0.0000 1.0000 0.0000
vn 0.0000 0.0000 1.0000
vn -1.0000 0.0000 0.0000
vn 1.0000 0.0000 0.0000
vn 0.0000 -1.0000 0.0000
usemtl mat1
# no texture coordinates
f 6//1 5//1 1//1 2//1
usemtl mat2
f 1/5/2 5/6/2 7/7/2 3/8/2
usemtl mat3
f 4/9/3 3/10/3 7/11/3 8/12/3
usemtl mat4
f 8/12/4 7/11/4 5/13/4 6/14/4
usemtl mat5
f 2/15/5 1/16/5 3/17/5 4/18/5
usemtl mat6
# no normals
f 6/14 2/4 4/19 8/20
'''
with open('test_cube.obj','w') as obj:
obj.write( data )
obj = load_obj( 'test_cube.obj' )
save_obj( obj, 'dump.obj' )
if __name__ == '__main__':
obj_load_save_example()
Hope it's useful!
Nov 05, 2019
These are collections of functions that I end up re-implementing frequently.
import numpy as np
def manifold_mesh_neighbors( tris: np.ndarray ) -> np.ndarray:
"""Returns an array of triangles neighboring each triangle
Args:
tris (Nx3 int array): triangle vertex indices
Returns:
nbrs (Nx3 int array): neighbor triangle indices,
or -1 if boundary edge
"""
if tris.shape[1] != 3:
raise ValueError('Expected a Nx3 array of triangle vertex indices')
e2t = {}
for idx,(a,b,c) in enumerate(tris):
e2t[(b,a)] = idx
e2t[(c,b)] = idx
e2t[(a,c)] = idx
nbr = np.full(tris.shape,-1,int)
for idx,(a,b,c) in enumerate(tris):
nbr[idx,0] = e2t[(a,b)] if (a,b) in e2t else -1
nbr[idx,1] = e2t[(b,c)] if (b,c) in e2t else -1
nbr[idx,2] = e2t[(c,a)] if (c,a) in e2t else -1
return nbr
if __name__ == '__main__':
tris = np.array((
(0,1,2),
(0,2,3)
),int)
nbrs = manifold_mesh_neighbors( tris )
tar = np.array((
(-1,-1,1),
(0,-1,-1)
),int)
if not np.allclose(nbrs,tar):
raise ValueError('uh oh.')
Nov 04, 2019
These are collections of functions that I end up re-implementing frequently.
from typing import *
import numpy as np
def closest_rotation( M: np.ndarray ):
U,s,Vt = np.linalg.svd( M[:3,:3] )
if np.linalg.det(U@Vt) < 0:
Vt[2] *= -1.0
return U@Vt
def mat2quat( M: np.ndarray ):
if np.abs(np.linalg.det(M[:3,:3])-1.0) > 1e-5:
raise ValueError('Matrix determinant is not 1')
if np.abs( np.linalg.norm( M[:3,:3].T@M[:3,:3] - np.eye(3)) ) > 1e-5:
raise ValueError('Matrix is not orthogonal')
w = np.sqrt( 1.0 + M[0,0]+M[1,1]+M[2,2])/2.0
x = (M[2,1]-M[1,2])/(4*w)
y = (M[0,2]-M[2,0])/(4*w)
z = (M[1,0]-M[0,1])/(4*w)
return np.array((x,y,z,w),float)
def quat2mat( q: np.ndarray ):
qx,qy,qz,qw = q/np.linalg.norm(q)
return np.array((
(1 - 2*qy*qy - 2*qz*qz, 2*qx*qy - 2*qz*qw, 2*qx*qz + 2*qy*qw),
( 2*qx*qy + 2*qz*qw, 1 - 2*qx*qx - 2*qz*qz, 2*qy*qz - 2*qx*qw),
( 2*qx*qz - 2*qy*qw, 2*qy*qz + 2*qx*qw, 1 - 2*qx*qx - 2*qy*qy),
))
if __name__ == '__main__':
for i in range( 1000 ):
q = np.random.standard_normal(4)
q /= np.linalg.norm(q)
A = quat2mat( q )
s = mat2quat( A )
if np.linalg.norm( s-q ) > 1e-6 and np.linalg.norm( s+q ) > 1e-6:
raise ValueError('uh oh.')
R = closest_rotation( A+np.random.standard_normal((3,3))*1e-6 )
if np.linalg.norm(A-R) > 1e-5:
print( np.linalg.norm( A-R ) )
raise ValueError('uh oh.')
Nov 03, 2019
Python is a pretty nice language for prototyping and (with numpy and scipy) can be quite fast for numerics but is not great for algorithms with frequent tight loops. One place I run into this frequently is in graphics, particularly applications involving meshes.
Not much can be done if you need to frequently modify mesh structure. Luckily, many algorithms operate on meshes with fixed structure. In this case, expressing algorithms in terms of block operations can be much faster. Actually implementing methods in this way can be tricky though.
To gain more experience in this, I decided to try implementing the As-Rigid-As-Possible Surface Modeling mesh deformation algorithm in Python. This involves solving moderately sized Laplace systems where the right-hand-side involves some non-trivial computation (per-vertex SVDs embedded within evaluation of the Laplace operator). For details on the algorithm, see the link.
As it turns out, the entire implementation ended up being just 99 lines and solves 1600 vertex problems in just under 20ms (more on this later). Full code is available.
Building the Laplace operator
ARAP uses cotangent weights for the Laplace operator in order to be relatively independent of mesh grading. These weights are functions of the angles opposite the edges emanating from each vertex. Building this operator using loops is slow but can be sped up considerably by realizing that every triangle has exactly 3 vertices, 3 angles and 3 edges. Operations can be evaluated on triangles and accumulated to edges.
Here's the Python code for a cotangent Laplace operator:
from typing import *
import numpy as np
import scipy.sparse as sparse
import scipy.sparse.linalg as spla
def build_cotan_laplacian( points: np.ndarray, tris: np.ndarray ):
a,b,c = (tris[:,0],tris[:,1],tris[:,2])
A = np.take( points, a, axis=1 )
B = np.take( points, b, axis=1 )
C = np.take( points, c, axis=1 )
eab,ebc,eca = (B-A, C-B, A-C)
eab = eab/np.linalg.norm(eab,axis=0)[None,:]
ebc = ebc/np.linalg.norm(ebc,axis=0)[None,:]
eca = eca/np.linalg.norm(eca,axis=0)[None,:]
alpha = np.arccos( -np.sum(eca*eab,axis=0) )
beta = np.arccos( -np.sum(eab*ebc,axis=0) )
gamma = np.arccos( -np.sum(ebc*eca,axis=0) )
wab,wbc,wca = ( 1.0/np.tan(gamma), 1.0/np.tan(alpha), 1.0/np.tan(beta) )
rows = np.concatenate(( a, b, a, b, b, c, b, c, c, a, c, a ), axis=0 )
cols = np.concatenate(( a, b, b, a, b, c, c, b, c, a, a, c ), axis=0 )
vals = np.concatenate(( wab, wab,-wab,-wab, wbc, wbc,-wbc,-wbc, wca, wca,-wca, -wca), axis=0 )
L = sparse.coo_matrix((vals,(rows,cols)),shape=(points.shape[1],points.shape[1]), dtype=float).tocsc()
return L
Inputs are float \(3 \times N_{verts}\) and integer \(N_{tris} \times 3\) arrays for vertices and triangles respectively. The code works by making arrays containing vertex indices and positions for all triangles, then computes and normalizes edges and finally computes angles and cotangents. Once the cotangents are available, initialization arrays for a scipy.sparse.coo_matrix are constructed and the matrix built. The coo_matrix is intended for finite-element matrices so it accumulates rather than overwrites duplicate values. The code is definitely faster and most likely fewer lines than a loop based implementation.
Evaluating the Right-Hand-side
The Laplace operator is just a warm-up exercise compared to the right-hand-side computation. This involves:
- For every vertex, collecting the edge-vectors in its one-ring in both original and deformed coordinates
- Computing the rotation matrices that optimally aligns these neighborhoods, weighted by the Laplacian edge weights, per-vertex. This involves a SVD per-vertex.
- Rotating the undeformed neighborhoods by the per-vertex rotation and summing the contributions.
In order to vectorize this, I constructed neighbor and weight arrays for the Laplace operator. These store the neighboring vertex indices and the corresponding (positive) weights from the Laplace operator. A catch is that vertices have different numbers of neighbors. To address this I use fixed sized arrays based on the maximum valence in the mesh. These are initialized with default values of the vertex ids and weights of zero so that unused vertices contribute nothing and do not affect matrix structure.
To compute the rotation matrices, I used some index magic to accumulate the weighted neighborhoods and rely on numpy's batch SVD operation to vectorize over all vertices. Finally, I used the same index magic to rotate the neighborhoods and accumulate the right-hand-side.
The code to accumulate the neighbor and weight arrays is:
def build_weights_and_adjacency( points: np.ndarray, tris: np.ndarray, L: Optional[sparse.csc_matrix]=None ):
L = L if L is not None else build_cotan_laplacian( points, tris )
n_pnts, n_nbrs = (points.shape[1], L.getnnz(axis=0).max()-1)
nbrs = np.ones((n_pnts,n_nbrs),dtype=int)*np.arange(n_pnts,dtype=int)[:,None]
wgts = np.zeros((n_pnts,n_nbrs),dtype=float)
for idx,col in enumerate(L):
msk = col.indices != idx
indices = col.indices[msk]
values = col.data[msk]
nbrs[idx,:len(indices)] = indices
wgts[idx,:len(indices)] = -values
Rather than break down all the other steps individually, here is the code for an ARAP class:
class ARAP:
def __init__( self, points: np.ndarray, tris: np.ndarray, anchors: List[int], anchor_weight: Optional[float]=10.0, L: Optional[sparse.csc_matrix]=None ):
self._pnts = points.copy()
self._tris = tris.copy()
self._nbrs, self._wgts, self._L = build_weights_and_adjacency( self._pnts, self._tris, L )
self._anchors = list(anchors)
self._anc_wgt = anchor_weight
E = sparse.dok_matrix((self.n_pnts,self.n_pnts),dtype=float)
for i in anchors:
E[i,i] = 1.0
E = E.tocsc()
self._solver = spla.factorized( ( self._L.T@self._L + self._anc_wgt*E.T@E).tocsc() )
@property
def n_pnts( self ):
return self._pnts.shape[1]
@property
def n_dims( self ):
return self._pnts.shape[0]
def __call__( self, anchors: Dict[int,Tuple[float,float,float]], num_iters: Optional[int]=4 ):
con_rhs = self._build_constraint_rhs(anchors)
R = np.array([np.eye(self.n_dims) for _ in range(self.n_pnts)])
def_points = self._solver( self._L.T@self._build_rhs(R) + self._anc_wgt*con_rhs )
for i in range(num_iters):
R = self._estimate_rotations( def_points.T )
def_points = self._solver( self._L.T@self._build_rhs(R) + self._anc_wgt*con_rhs )
return def_points.T
def _estimate_rotations( self, def_pnts: np.ndarray ):
tru_hood = (np.take( self._pnts, self._nbrs, axis=1 ).transpose((1,0,2)) - self._pnts.T[...,None])*self._wgts[:,None,:]
rot_hood = (np.take( def_pnts, self._nbrs, axis=1 ).transpose((1,0,2)) - def_pnts.T[...,None])
U,s,Vt = np.linalg.svd( rot_hood@tru_hood.transpose((0,2,1)) )
R = U@Vt
dets = np.linalg.det(R)
Vt[:,self.n_dims-1,:] *= dets[:,None]
R = U@Vt
return R
def _build_rhs( self, rotations: np.ndarray ):
R = (np.take( rotations, self._nbrs, axis=0 )+rotations[:,None])*0.5
tru_hood = (self._pnts.T[...,None]-np.take( self._pnts, self._nbrs, axis=1 ).transpose((1,0,2)))*self._wgts[:,None,:]
rhs = np.sum( (R@tru_hood.transpose((0,2,1))[...,None]).squeeze(), axis=1 )
return rhs
def _build_constraint_rhs( self, anchors: Dict[int,Tuple[float,float,float]] ):
f = np.zeros((self.n_pnts,self.n_dims),dtype=float)
f[self._anchors,:] = np.take( self._pnts, self._anchors, axis=1 ).T
for i,v in anchors.items():
if i not in self._anchors:
raise ValueError('Supplied anchor was not included in list provided at construction!')
f[i,:] = v
return f
The indexing was tricky to figure out. Error handling and input checking can obviously be improved. Something I'm not going into are the handling of anchor vertices and the overall quadratic forms that are being solved.
So does it Work?
Yes. Here is a 2D equivalent to the bar example from the paper:
import time
import numpy as np
import matplotlib.pyplot as plt
import arap
def grid_mesh_2d( nx, ny, h ):
x,y = np.meshgrid( np.linspace(0.0,(nx-1)*h,nx), np.linspace(0.0,(ny-1)*h,ny))
idx = np.arange(nx*ny,dtype=int).reshape((ny,nx))
quads = np.column_stack(( idx[:-1,:-1].flat, idx[1:,:-1].flat, idx[1:,1:].flat, idx[:-1,1:].flat ))
tris = np.vstack((quads[:,(0,1,2)],quads[:,(0,2,3)]))
return np.row_stack((x.flat,y.flat)), tris, idx
nx,ny,h = (21,5,0.1)
pnts, tris, ix = grid_mesh_2d( nx,ny,h )
anchors = {}
for i in range(ny):
anchors[ix[i,0]] = ( 0.0, i*h)
anchors[ix[i,1]] = ( h, i*h)
anchors[ix[i,nx-2]] = (h*nx*0.5-h, h*nx*0.5+i*h)
anchors[ix[i,nx-1]] = ( h*nx*0.5, h*nx*0.5+i*h)
deformer = arap.ARAP( pnts, tris, anchors.keys(), anchor_weight=1000 )
start = time.time()
def_pnts = deformer( anchors, num_iters=2 )
end = time.time()
plt.triplot( pnts[0], pnts[1], tris, 'k-', label='original' )
plt.triplot( def_pnts[0], def_pnts[1], tris, 'r-', label='deformed' )
plt.legend()
plt.title('deformed in {:0.2f}ms'.format((end-start)*1000.0))
plt.show()
The result of this script is the following:
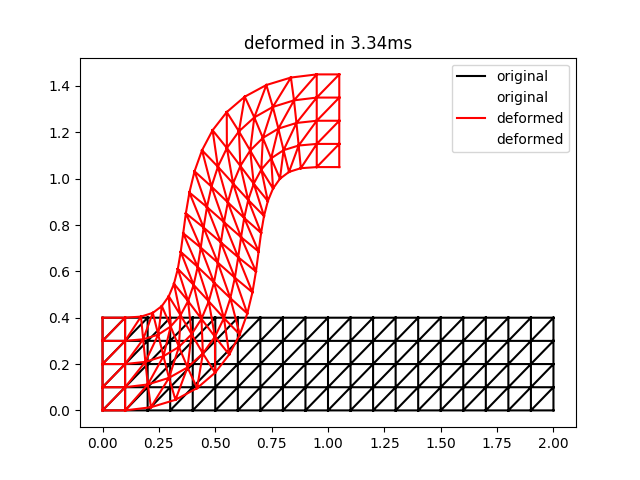
This is qualitatively quite close to the result for two iterations in Figure 3 of the ARAP paper. Note that the timings may be a bit unreliable for such a small problem size.
A corresponding result for 3D deformations is here (note that this corrects an earlier bug in rotation computations for 3D):

Mar 09, 2019
Projection of known 3D points into a pinhole camera can be modeled by the following equation:
\begin{align*}
\begin{bmatrix} \hat{u}_c \\ \hat{v}_c \\ \hat{w}_c \end{bmatrix}
= \begin{bmatrix} f & 0 & u_0 \\ 0 & f & v_0 \\ 0 & 0 & 1 \end{bmatrix}
\begin{bmatrix}
r_{xx} & r_{xy} & r_{xz} & t_x \\
r_{yx} & r_{yy} & r_{yz} & t_y \\
r_{zx} & r_{zy} & r_{zz} & t_z
\end{bmatrix} \begin{bmatrix} x_w \\ y_w \\ z_w \\ 1 \end{bmatrix} \\
= K E x
\end{align*}
The matrix \(K\) contains the camera intrinsics and the matrix \(E\) contains the camera extrinsics. The final image coordinates are obtained by perspective division: \(u_c = \hat{u}_c/\hat{w}_c\) and \(v_c = \hat{v}_c/\hat{w}_c\).
Estimating \(K\) and \(E\) jointly can be difficult because the equations are non-linear and may converge slowly or to a poor solution. Tsai's algorithm provides a way to obtain initial estimates of the parameters for subsequent refinement. It requires a known calibration target that can be either planar or three-dimensional.
The key step is in estimating the rotation and x-y translation of the extrinsics \(E\) in such a way that the unknown focal length is eliminated. Once the rotation is known, the focal-length and z translation can be computed.
This process requires the optical center \([u_0, v_0]\) which is also unknown. However, given reasonable quality optics this is often near the image center so the center can be used as an initial estimate.
This is the starting point for the estimation.
Estimating (most of) the Extrinsics
This is divided into two cases, one for planar targets and one for 3D targets.
Case 1: 3D Non-planar Target:
For calibration targets with 8+ points that span 3 dimensions. Points in the camera frame prior to projection are:
\begin{equation*}
\begin{bmatrix} x_c \\ y_c \\ z_c \end{bmatrix} =
\begin{bmatrix}
r_{xx} x_w + r_{xy} y_w + r_{xz} z_w + t_x \\
r_{yx} x_w + r_{yy} y_w + r_{yz} z_w + t_y \\
r_{zx} x_w + r_{zy} y_w + r_{zz} z_w + t_z
\end{bmatrix}
\end{equation*}
The image points relative to the optical center are then:
\begin{equation*}
\begin{bmatrix} u_c - u_0 \\ v_c - v_0 \end{bmatrix} =
\begin{bmatrix} u_c' \\ v_c' \end{bmatrix} =
\begin{bmatrix}
(f x_c + u_0 z_c)/z_c - u_0 \\
(f y_c + v_0 z_c)/z_c - v_0
\end{bmatrix} =
\begin{bmatrix}
f x_c/z_c \\
f y_c/z_c
\end{bmatrix}
\end{equation*}
The ratio of these two quantities gives the equation:
\begin{equation*}
\frac{u_c'}{v_c'} = \frac{x_c}{y_c}
\end{equation*}
or, after cross-multiplying and collecting terms to one side:
\begin{align*}
v_c' x_c - u_c' y_c = 0 \\
[ v_c' x_w, v_c' y_w, v_c' z_w, -u_c' x_w, -u_c' y_w, -u_c' z_w, 1, -1] \begin{bmatrix}
r_{xx} \\ r_{xy} \\ r_{xz} \\ r_{yx} \\ r_{yy} \\ r_{yz} \\ t_x \\ t_y
\end{bmatrix} = 0
\end{align*}
Each point produces a single equation like the above which can be stacked to form a homogeneous system. With a zero right-hand-side, scalar multiples of the solution still satisfy the equations and a trivial all-zero solution exists. Calling the system matrix \(M\), the solution to this equation system is the eigenvector associated with the smallest eigenvalue of \(M^T M\). The computed solution will be proportional to the desired solution. It is also possible to fix one value, e.g. \(t_y=1\) and solve an inhomogeneous system but this may give problems if \(t_y \neq 0\) for the camera configuration.
The recovered \(r_x = [ r_{xx}, r_{xy}, r_{xz} ]\) and \(r_x = [ r_{yx}, r_{yy}, r_{yz} ]\) should be unit length. The scale of the solution can be recovered as the mean length of these vectors and used to inversely scale the translations \(t_x, t_y\).
Case 2: 2D Planar Targets:
For 2D targets, arbitrarily set \(z_w=0\), leading to:
\begin{equation*}
\begin{bmatrix} x_c \\ y_c \\ z_c \end{bmatrix} =
\begin{bmatrix}
r_{xx} x_w + r_{xy} y_w + t_x \\
r_{yx} x_w + r_{yy} y_w + t_y \\
r_{zx} x_w + r_{zy} y_w + t_z
\end{bmatrix}
\end{equation*}
Use the same process as before, a homogeneous system can be formed. It is identical to the previous one, except the \(r_{xz}\) and \(r_{yz}\) terms are dropped since \(z_w=0\). Each equation ends up being:
\begin{equation*}
[ v_c' x_w, v_c' y_w, -u_c' x_w, -u_c' y_w, 1, -1] \begin{bmatrix}
r_{xx} \\ r_{xy} \\ r_{yx} \\ r_{yy} \\ t_x \\ t_y
\end{bmatrix} = 0
\end{equation*}
Solving this gives \(r_{xx}, r_{xy}, r_{zx}, r_{zy}, t_x, t_y\) up to a scalar \(k\). It does not provide \(r_{xz}, r_{yz}\). In addition, we know that the rows of the rotation submatrix are unit-norm and orthogonal, giving three equations:
\begin{align*}
r_{xx}^2 + r_{xy}^2 + r_{xz}^2 = k^2 \\
r_{yz}^2 + r_{yy}^2 + r_{yz}^2 = k^2 \\
r_{xx} r_{yx} + r_{xy} r_{yy} + r_{xz} r_{yz} = 0
\end{align*}
After some algebraic manipulations the factor \(k^2\) can be found as:
\begin{equation*}
k^2 = \frac{1}{2}\left( r_{xx}^2 + r_{xy}^2 + r_{yx}^2 + r_{yy}^2 + \sqrt{\left( (r_{xx} - r_{yy})^2 + (r_{xy} + r_{yx})^2\right)\left( (r_{xx}+r_{yy})^2 + (r_{xy} - r_{yx})^2 \right) } \right)
\end{equation*}
This allows \(r_{xz}, r_{yz}\) to be found as:
\begin{align*}
r_{xz} = \pm\sqrt{ k^2 - r_{xx}^2 - r_{xy}^2 } \\
r_{yz} = \pm\sqrt{ k^2 - r_{yz}^2 - r_{yy}^2 }
\end{align*}
Estimate Remaining Intrinsics and Focal Length
Estimating the focal length and z-translation follows a similar process. Using the definitions above we have:
\begin{align*}
u_c' = f \frac{x_c}{z_c} \\
v_c' = f \frac{y_c}{z_c}
\end{align*}
Cross-multiplying and collecting gives:
\begin{align*}
(r_{xx} x_w + r_{xy} y_w + r_{xz} z_w + t_x) f - u_c' t_z = u_c' (r_{zx} x_w + r_{zy} y_w + r_{zz} z_w) \\
(r_{yx} x_w + r_{yy} y_w + r_{yz} z_w + t_y) f - v_c' t_z = v_c' (r_{zx} x_w + r_{zy} y_w + r_{zz} z_w)
\end{align*}
Solving this system gives the desired \(f, t_x\) values.


